Рассмотрим алгоритмы на примере следующей задачи Коши:
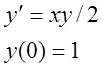
//Метод Эйлера с уравниванием
#include<stdio.h>
#include<math.h>
#define N 3
float f(float x, float y);
void main()
{ int k;
float h=0.1,x[N],y[N],y_[N],y_pr;
FILE *out;
out=fopen("out1.dan","w");
x[0]=0; y[0]=1; y_[0]=f(0,1);
k=0;
do
{ x[k+1]=x[0]+(k+1)*h;
y[k+1]=y[k]+y_[k]*h;
y_[k+1]=f(x[k+1],y[k+1]);
do
{ y_pr=y[k+1];
y[k+1]=y[k]+0.5*(y_[k]+y[k+1])*h;
y_[k+1]=f(x[k+1],y[k+1]);
}
while (y_pr!=y[k+1]);
k+=1;
}
while (k<N-1);
for(k=0;k<N;k++)
fprintf(out,"x=%g y=%f\n",x[k],y[k]);
}
float f(float x,float y)
{ return (x*y/2);
}
//Формула Адамса с первыми разностями
#include<stdio.h>
#include<math.h>
#define N 11
float f(float x, float y);
void main()
{ int k;
float h=0.1,x[N],y[N],q[N],dq;
FILE *out;
out=fopen("out2.dan","w");
x[0]=0; y[0]=1; y[1]=1.007588; y[2]=1.012632; q[0]=f(x[0],y[0])*h;
for (k=1;k<N;k++)
x[k]=x[0]+k*h;
for (k=1;k<N-1;k++)
{ q[k]=f(x[k],y[k])*h;
dq=q[k]-q[k-1];
y[k+1]=y[k]+q[k]+0.5*dq;
}
for(k=0;k<N;k++)
fprintf(out,"x=%g y=%f\n",x[k],y[k]);
}
float f(float x,float y)
{ return (x*y/2);
}
//Формула Адамса со вторыми разностями
#include<stdio.h>
#include<math.h>
#define N 11
float f(float x, float y);
void main()
{ int k;
float h=0.1,x[N],y[N],q[N-1],dq[N-2],ddq[N-3];
FILE *out;
out=fopen("out3.dan","w");
x[0]=0; y[0]=1; y[1]=1.007588; y[2]=1.012632;
q[0]=f(x[0],y[0])*h; q[1]=f(x[1],y[1])*h;
dq[0]=q[1]-q[0];
for (k=1;k<N;k++)
x[k]=x[0]+k*h;
for(k=2;k<N-1;k++)
{ q[k]=f(x[k],y[k])*h;
dq[k-1]=q[k]-q[k-1];
ddq[k-2]=dq[k-1]-dq[k-2];
y[k+1]=y[k]+q[k]+0.5*dq[k-1]+5*ddq[k-2]/12;
}
for(k=0;k<N;k++)
fprintf(out,"x=%g y=%f\n",x[k],y[k]);
}
float f(float x,float y)
{ return (x*y/2);
}
//Метод А.Н.Крылова
#include<stdio.h>
#include<math.h>
#define N 3
float f(float x, float y);
void main()
{ int k=1; //номер приближения
float h=0.1,x[N],y[N],dy[N-1],dyk[N-1],q[N-1],dq[N-2],ddq;
FILE *out;
out=fopen("out4.dan","w");
x[0]=0; y[0]=1;
q[0]=f(x[0],y[0])*h;
do
{ x[k]=x[0]+k*h;
y[1]=y[0]+q[0];
if (k>1)
y[1]+=dq[0]*0.5;
if (k>2)
y[1]-=ddq/12 ;
dy[0]=y[1]-y[0];
q[1]=f(x[1],y[1])*h;
dq[0]=q[1]-q[0];
if (k>1)
{ y[2]=y[1]+q[1]+0.5*dq[0];
if (k>2)
y[2]+=5*ddq/12;
dy[1]=y[2]-y[1];
if (k<3)
{ q[2]=f(x[2],y[2])*h;
dq[1]=q[2]-q[1];
ddq=dq[1]-dq[0];
}
}
k++;
}
while (k<4);
k=0;
do
{ fprintf(out,"x=%g y=%f\n",x[k],y[k]);
k++;
}
while (k<N);
}
float f(float x,float y)
{ return (x*y/2);
}
//Метод Адамса-Крылова
#include<stdio.h>
#include<math.h>
#define N 11
float f(float x, float y);
void main()
{ int k=1;
float h=0.1,x[N],y[N],dy[N-1],dyk[N-1],q[N-1],dq[N-2],ddq[N-3];
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.