Сумський Державний Університет
з дисципліни
“Теорія ймовірностей і математична статистика”
(п’ятий семестр)
МОДУЛЬ 3
Виконав: студент групи ІН-83
Мірошниченко В. М..
Перевірив: проф. Мазманішвілі О.С.
Суми – 2011
Густина розподілу ![]() випадкової величини X має вигляд
випадкової величини X має вигляд
![]() ,
, ![]() .
.
В задачі потрібно:
1. Знайти сталу ![]() .
.
2. Знайти математичне сподівання ![]() .
.
3. Розглянувши випадкові події ![]() та
та ![]() ,
знайти ймовірності
,
знайти ймовірності ![]() ,
, ![]() та їх
відношення
та їх
відношення ![]() .
.
4. Оформити результати графічно.
Параметри:
k = 0, m = 0, n =2, p = 2.
Підставимо задані
параметри і отримаємо густину розподілу ![]() випадкової величини X, яка має вигляд:
випадкової величини X, яка має вигляд:
![]() ,
, ![]()
1. Знайти
сталу ![]() .
.
Густина f(x) будь-якої випадкової величини невід'ємна, f(x) > 0, та має властивість
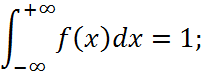
тобто ймовірність повної групи подій дорівнює одиниці.
Коефіцієнт С визначимо за допомогою формули про ймовірність повної групи подій:
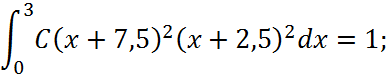
Зробимо заміну:
![]()
![]()
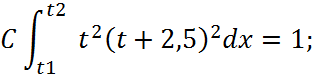
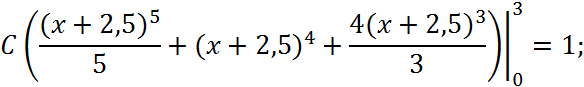
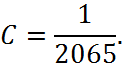
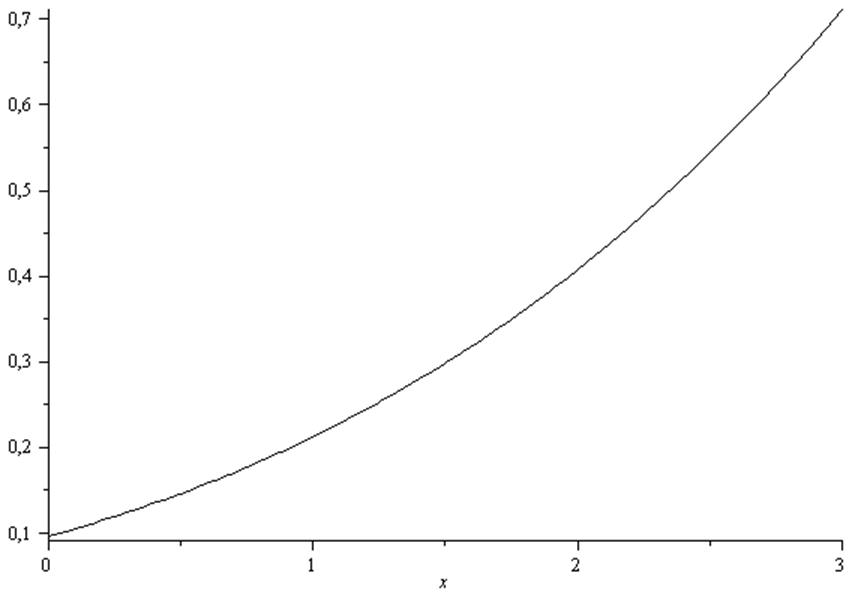
Рис.1 – графік густини розподілу
2.
Знайти математичне сподівання ![]() .
.
Математичним сподіванням неперервної випадкової величини X з густиною f(x) називається її середнє значення, що обчислюється за формулою
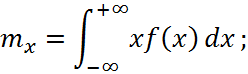
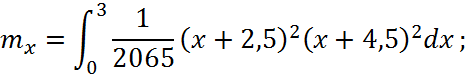
Зробимо заміну:
![]()
![]()
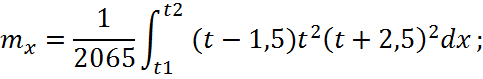
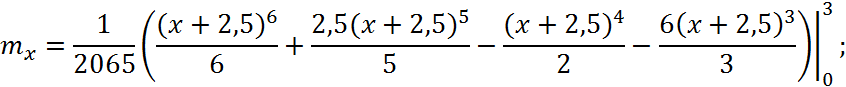
![]()
3.
Розглянемо подію ![]() .
Оскільки, за умовою
.
Оскільки, за умовою ![]() то
розіб’ємо інтервал на дві частини по
то
розіб’ємо інтервал на дві частини по ![]() .
Отримаємо, що
.
Отримаємо, що ![]() і
і
![]() . Тоді у термінах інтегральної функції
розподілу
. Тоді у термінах інтегральної функції
розподілу ![]() буде обчислюватися як:
буде обчислюватися як:
![]()
І аналогічно обчислюється ![]() :
:
![]()
Спочатку знайдемо F(x):
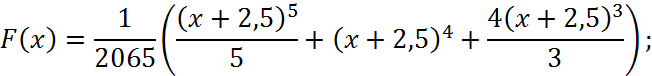
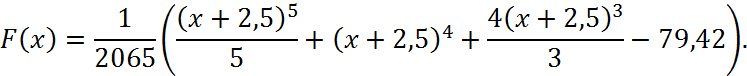
Обчислимо ймовірність ![]() :
:
![]()
Тепер знайдемо ймовірність ![]() :
:
![]()
Отже,
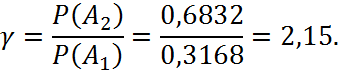
Передбачається, що один з двох приладів, які визначають швидкість автомобіля, має систематичну помилку (завищення). Для перевірки цього припущення визначили швидкість 10 автомобілів, причому швидкість кожного з них фіксувалася одночасно двома приладами. У результат отримані наступні дані:
|
|
70 |
85 |
63 |
54 |
65 |
80 |
75 |
95 |
52 |
55 |
|
|
72 |
86 |
62 |
55 |
63 |
80 |
78 |
90 |
53 |
57 |
Чи дозволяють ці дані стверджувати,
що другий прилад дійсно дає завищені значення швидкості? Прийняти ![]() =0,05.
=0,05.
Н0 : другий прилад дійсно дає завищені значення швидкості.
Перевіримо гіпотезу H0 про те, що прилад дійсно дає завищені значення швидкості.
Знайдемо вибіркові середні для
величин ![]() . Позначимо їх через x та у відповідно.
. Позначимо їх через x та у відповідно.
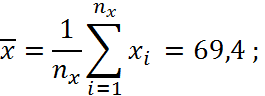
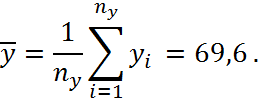
Знайдемо вибіркові дисперсії:
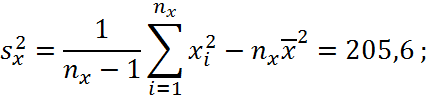
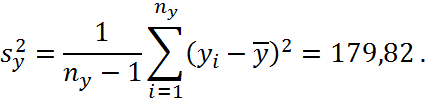
Знайдемо середньоквадратичне відхилення:
sx=14.3;
sy=13,40.
Знайдемо довірчі інтервали для математичного сподівання ![]() генеральної сукупності:
генеральної сукупності:
![]()
![]() – середнє;
– середнє;
![]() – точність.
– точність.
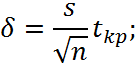
![]() – квантиль розподілу Ст’юдента.
– квантиль розподілу Ст’юдента.
![]()
![]()
![]()
![]()
Ми бачимо, що другий прилад дійсно може давати завищення з надійністю γ=0,95.
Знайдемо довірчі інтервали для генеральних дисперсій ![]() та
та ![]() :
:
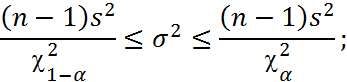
χ2 – квантиль розподілу Пірсона.
![]()
![]()
Інтервали перетинаються, тому з імовірністю 95% ми не можемо відкинути гіпотезу про рівність дисперсій, отже, другий прилад не дає завищення.
Відповіть: гіпотеза Н0
відкидається, з рівнем значущості ![]() =0,05.
=0,05.
На протязі деякого терміну фіксувалась кількість аварій водогінної мережі міста. Отримано наступні дані:
|
Кількість аварій, X |
0 |
1 |
2 |
3 |
4 |
5 |
|
Частоти, |
8 |
28 |
31 |
18 |
9 |
6 |
Перевірити гіпотезу про то, що
розподіл кількості аварі водогінної мережі міста підпорядковується закону
Пуассона. Рівень значущості прийнять ![]() =0,10 та
=0,10 та ![]() =0,05. Результати оформіть графічно.
=0,05. Результати оформіть графічно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.