Розв’язання задач на пошук сталої, математичного сподівання, ймовірності та їх відношення, страница 2

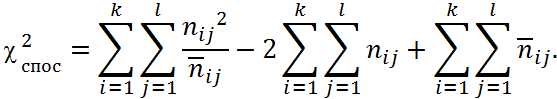
В цьому виразі другий доданок дорівнює 2n, третій доданок дорівнює n, тому:

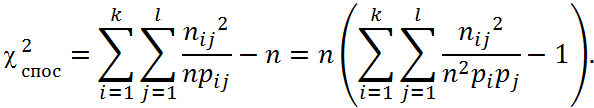
Приймемо для очікуваних ймовірностей, що pі = v_i/ n та р_j - = u_j/n, тоді після перетворень, запишемо:

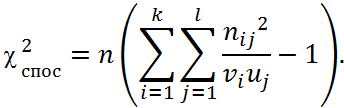
За умови, що гіпотеза Н₀ вірна, статистика має розподіл χ²  з (k-1)(l-1) ступенями вільності. Параметри к і l дорівнюють к = 3 і l = 2, так що повна кількість ступенів вільності становить:

v=(к-1)(1-1)= 2.

Користуючись формулою, знайдемо:

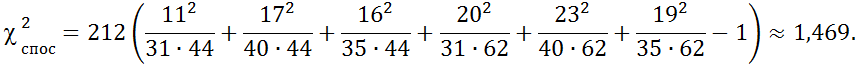
Для перевірки гіпотези порівняємо знайдене значення з критичним, знайдемо критичне значення  за формулою

За таблицею квантилів  χ² - розподілу знаходимо:

При α=0,1, ;

При α=0,05, .

Оскільки  , то при даному рівні значущості Н₀ приймається, з формулюванням, що експерементні дані не суперечать гіпотезі. Отже, потрібно вважати, що результат дії ліків не залежить від способу їх застосування.

Відповідь

Результат дії ліків не залежить від способу їх застосування.

Задача 4

Нижче наводиться час (в секундах) розв'язання контрольних задач учнями до i після спеціальних вправ по усному рахунку.

До вправ	87	61	98	90	74	83	72	81	75	83	85
Після вправ	50	45	79	88	65	52	79	84	61	52	85

Чи можна вважати, що ці вправи поліпшили здатність учнів в розв’язанні задач? Прийняти =0,10 та =0,05.

Розв’язання

Час необхідний для розв’язання завдань до і після вправ вважаємо випадковою величиною розподіленою за нормальним законом

 n₁=n₂ = 11при цьому невідомі, а хоч і невідомі але вважається що вони рівні.

          Згідно з умовою нам необхідно перевірити нульову гіпотезу

{H₀ : a₁ = a₂ } – середній час вирішення завдань до і після вправ є рівним,

{H₁ : a₁ < a₂ } – середній час вирішення завдань покращився, тобто зменшився.

          Так як об’єм вибірки малий то для перевірки нульової гіпотези застосуємо правосторонній t-критерій. Для цього проведемо додаткові обчислення:

i	xi	(xi-xs)2	yi	(yi-ys)2
1	87	38,21488	50	298,3471
2	61	392,7603	45	496,0744
3	98	295,2149	79	137,5289
4	90	84,30579	88	429,6198
5	74	46,4876	65	5,165289
6	83	4,760331	52	233,2562
7	72	77,76033	79	137,5289
8	81	0,033058	84	279,8017
9	75	33,85124	61	39,34711
10	83	4,760331	52	233,2562
11	85	17,4876	85	314,2562
Сума	889	995,6364	740	2604,182
Середнє	80,81818	90,5124	67,27273	236,7438

З даних наведених у таблиці витікає s₁²=90,5124, s₁²=236,7438.

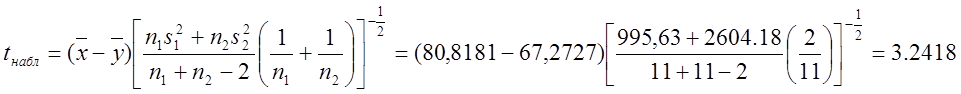Число степенів свободи v=20. За таблицею квантилей розподілу Ст’юдента знаходимо , .

Так як 2.086 < 3.2418  та 1.7247< 3.2418 ми відкидаємо нульову гіпотезу в обох випадках. Це означає що різниця середніх є статистично значущою.

Відповідь

Вправи покращили здатність учнів розв’язувати задачі

Задача 5

Обсяг продуктів (Y) за 1990–1997 рр. (X)  наведені в наступній таблиці:

X	1990	1991	1992	1993	1994	1995	1996	1997
Y в % к 1950 р.	100	116	122	134	144	165	180	219

Вважаючи, що залежність Y від X лінійна, ,  знайти параметри a та b за методом найменших квадратів. Вважаючи також, що залежність X від Y лінійна, , знайти параметри c та d за методом найменших квадратів. Виявити зв’язок між знайденими коефіцієнтами. Результати оформити графічно.

Розв’язання

При нанесенні експериментальних даних у вигляді точок у декартовій системі координат отримуємо кореляційне поле. Якщо є підстави вважати, що двовимірна випадкова величина (X,У) розподілена згідно з нормальним законом або якщо точки на кореляційному полі групуються навколо прямої лінії, то емпіричне рівняння регресії підбирається у вигляді

y=ax+b.

Наступна задача - знаходження коефіцієнтів (параметрів) a і b лінійних емпіричних функцій регресії Y на X. Шукатимемо ці параметри методом найменших квадратів, тобто прагнемо виконання умови мінімуму нев’язки:

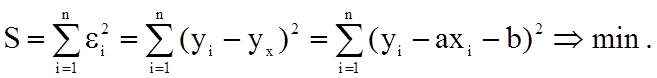
Оскільки функціонал нев'язки S в просторі параметрів a та b досягає мінімуму, то для визначення координат цього екстремуму маємо знайти часткові похідні ∂S/∂a, ∂S/∂b і прирівняти їх до нуля:

∂S/∂a=0;

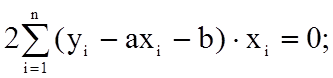
∂S/∂b=0;

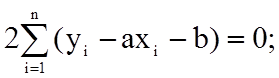
Отримуємо систему з двох лінійних рівнянь (тобто систему нормальних рівнянь):

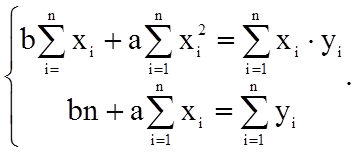
Розв'язуючи систему, знаходимо шукані коефіцієнти a та b. Якщо потрібно за експериментальними даними  розв'язати лінійне рівняння регресії X на Y вигляду:

x = cy+d,

то його коефіцієнти (параметри) c та d знаходять з розв'язку системи нормальних рівнянь:

Регресія y = ax+b:

;

 ;

;

;

;

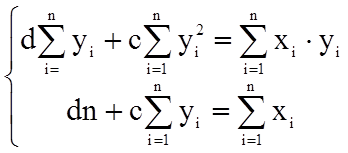
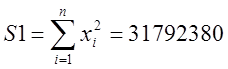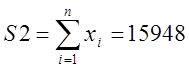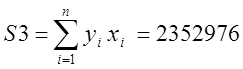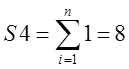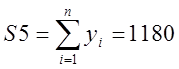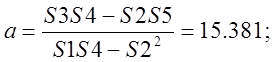
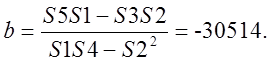
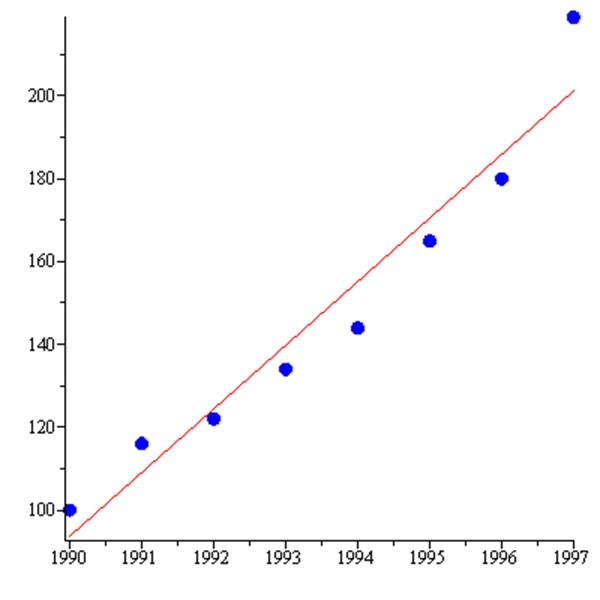
Рис. 3 - Графік рівняння регресії Х на Y

Регресія x = cy+d

;

 ;

;

;

;

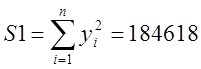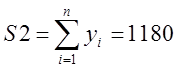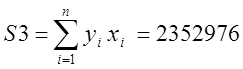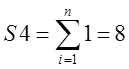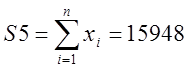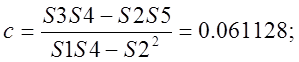
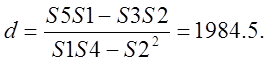
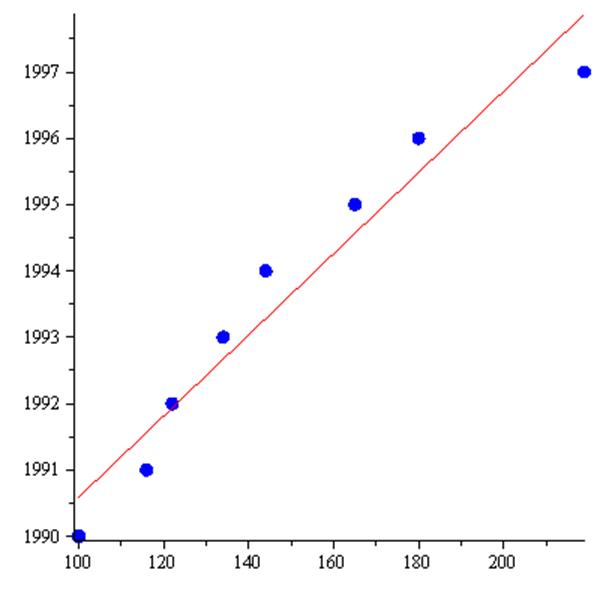
Рис. 4 - Графік рівняння регресії Y на X