Міністерство освіти та науки України
Сумський державний університет
Кафедра моделювання складних систем
Обов’язкове домашнє завдання №2
з дисципліни: «Теорія ймовірності та математична статистика»
Модуль 2
Варіант 21
підготувала
студентка групи ІН-83
Шамшина С. Ю.
перевірив
професор Мазманішвілі О. С.
Суми 2010
Завдання 1
Отримана вибірка
об’єму ![]() :
:
7, 1, 4+m, 3, 2+k, 16+2![]() , 15-n, 4, 1, 1, 3+k, 5,
, 15-n, 4, 1, 1, 3+k, 5,
5, 6, 6, 6, 1, 5+m, 3+n, 14-2m, 2, 2, 7, 7, 7, 4, 4,
3, 1, 2+p, 6, 8, 4, 15-3p, 1+k, 1+m, 1+n, 5, 5, 3.
В задачі потрібно:
1. Побудувати: інтервальний варіаційний ряд розподілу; гістограму; емпіричну функцію розподілу.
2. Знайти: вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення, медіану і моду вибірки.
3. Оформити результати графічно.
Номер варіанта Параметри
21 k = 2, m = 2, n = 3, p = 2, с = 0.
Розв’язання:
Згідно з варіантом вибірка має вигляд:
7, 1, 6, 3, 4, 16, 12, 4, 1, 1, 5, 5,
5, 6, 6, 6, 1, 7, 6, 10, 2, 2, 7, 7, 7, 4, 4,
3, 1, 4, 6, 8, 4, 9, 3, 3, 4, 5, 5, 3.
Запишемо вибірку наступним чином:
1, 1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5,
6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8,
9, 10, 12, 16.
1) Інтервальний варіаційний ряд розподілу:
|
Інтервал |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Частота |
5 |
2 |
5 |
7 |
5 |
6 |
5 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
2) Побудуємо гістограму:
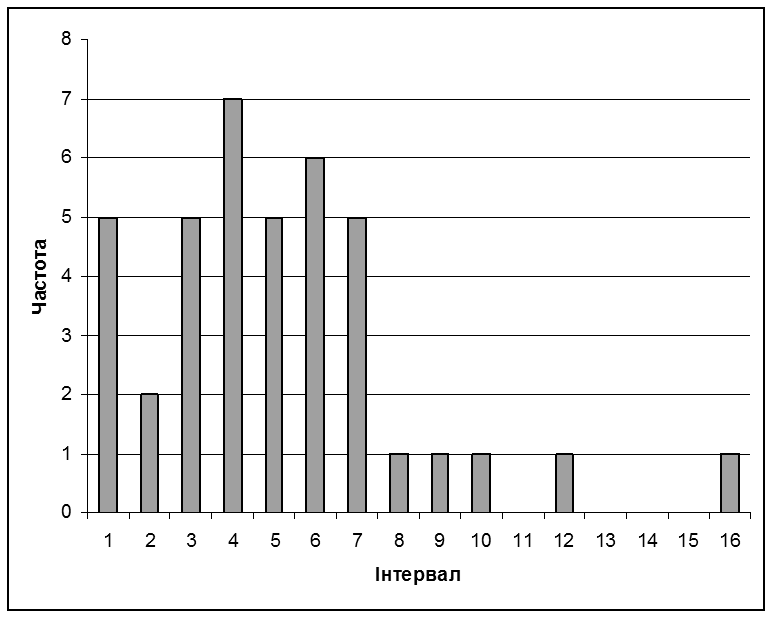
Рис. 1. Гістограма
3) Побудуємо емпіричну функцію розподілу:
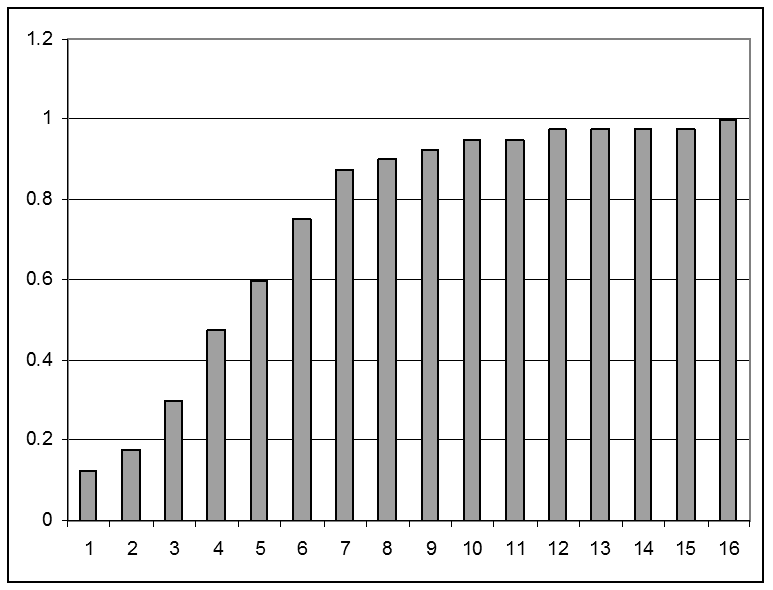
Рис. 2. Емпірична функція розподілу
4) Обчислимо вибіркове середнє, вибіркову дисперсія, середнє квадратичне відхилення, медіану і моду вибірки:
Вибіркове середнє:
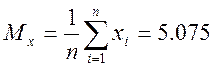 .
.
Вибіркова дисперсія:
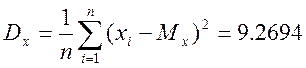 .
.
Середнє квадратичне відхилення:
![]() .
.
Медіана: ![]() .
.
Мода: ![]() .
.
Завдання 2
Випадкова величина Х задана густиною розподілу ймовірностей:
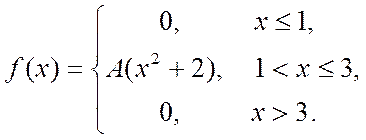
Знайти: параметр А; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність Pr(π/4≤X≤π).
Розв’язання:
1. Параметр А будемо шукати за умови, що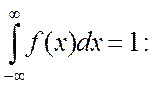
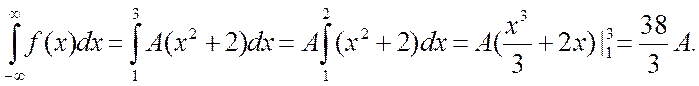
Звідси 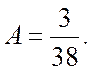
Отже, густина розподілу ймовірностей з урахуванням параметру А буде:
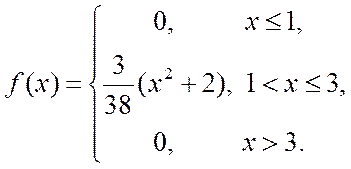
2. Оскільки задана функція густини ![]() знайдемо функцію розподілу
знайдемо функцію розподілу ![]()
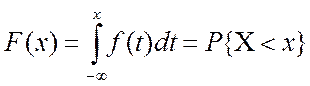 .
.
а) Розглянемо ділянку,
де ![]()
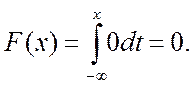
b) Розглянемо ділянку, де ![]()
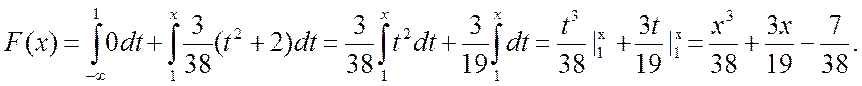
с) Розглянемо ділянку
де ![]()
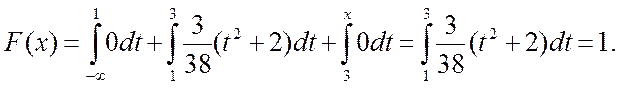
Отже, функція розподілу матиме наступний вигляд:
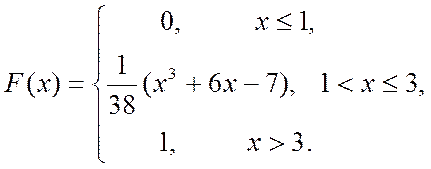
3. Математичне сподівання ![]() для
неперервних випадкових величин знаходиться як:
для
неперервних випадкових величин знаходиться як:
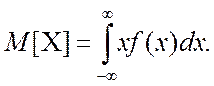
Для нашого випадку:
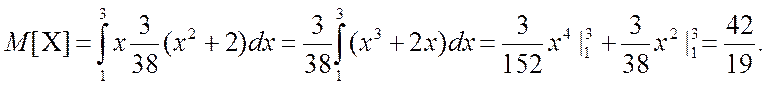
Отже
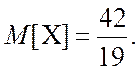
4.
Знайдемо дисперсію ![]() для неперервних випадкових величин, що
визначається як:
для неперервних випадкових величин, що
визначається як:
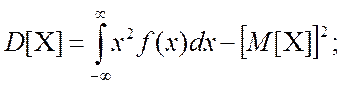
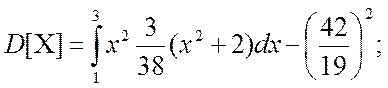
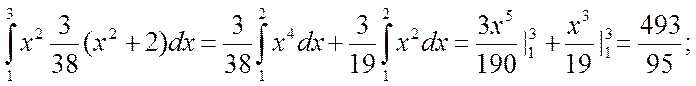
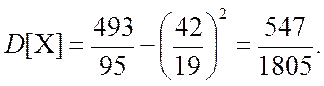
5. Знайдемо ймовірність події Pr(π/4≤X≤π), тобто ймовірність
попадання ![]() на проміжок [π/4,π]:
на проміжок [π/4,π]:
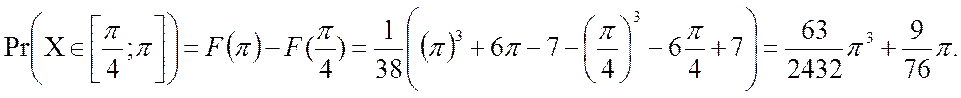
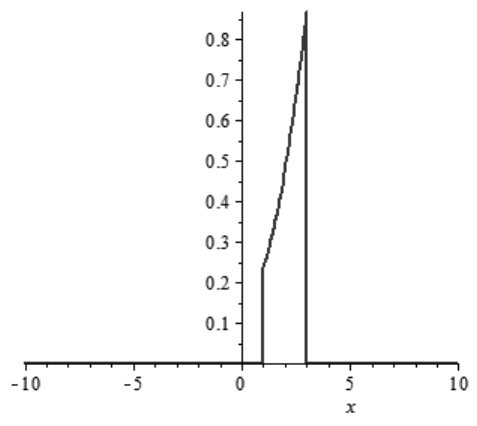
Рис. 3. Графік густини розподілу ![]()
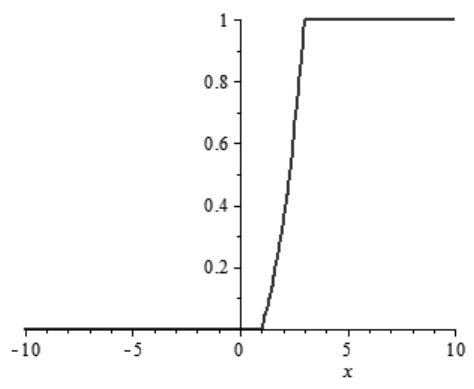
Рис. 4. Графік функції розподілу ![]()
Завдання 3:
На площині задано два круга радіусом R кожний. Центр першого круга знаходиться в точці (R,R). Центр другого круга знаходиться в початку координат.
Знайти ймовірність того, що точка, яка 10 раз наугад кинута в перший круг, влучить 2 разу з них також і в другий.
Розв’язання:

1. Визначимо площу спільної частини двох кругів:
Площа круга: ![]() .
.
Площа четвертої частини круга:
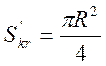 .
.
Площа квадрата, у якому знаходиться четверта частина круга:
![]() .
.
Різниця між площею четвертої частини круга та квадрату:
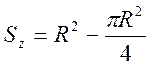 .
.
Отже, площа спільної частини двох кругів:
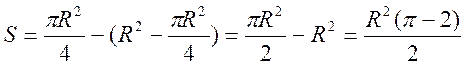 .
.
2. Визначимо ймовірність попадання наугад кинутої точки в перший круг в другий круг:
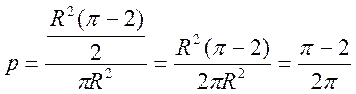 .
.
3. За формулою Бернуллі підрахуємо ймовірність попадання наугад кинутої точки 10 разів в перший круг 2 рази з них в другий:
![]() де
де ![]() ;
; ![]() ;
; ![]() .
.
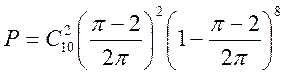 ;
;
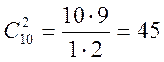 ;
;
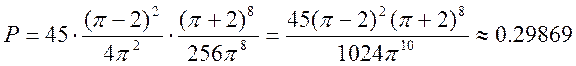 .
.
Відповідь: ймовірність того, що точка, яка 10 раз наугад кинута в перший круг, влучить
2 разу з них також і в другий, ![]() .
.
Завдання 4:
Знайти густину розподілу випадкової величині, якому відповідає характеристична
функція q(t)=cos![]() (t).
(t).
Розв’язання:
Густина розподілу випадкової величини:
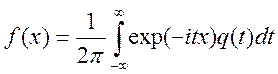 ;
;
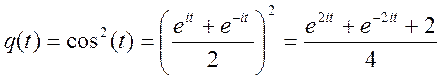 ;
;
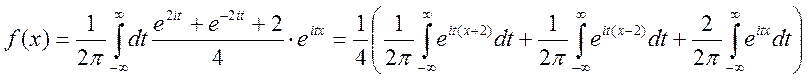 ;
;
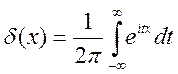 .
.
Отже
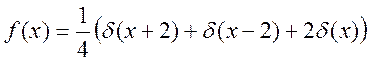 .
.
Відповідь: густина розподілу випадкової величини
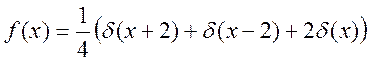 .
.
Завдання 5:
Система випадкових
величин (X,Y) має густину розподілу ![]() ,
, ![]() . Знайти густину розподілу
. Знайти густину розподілу ![]() випадкової величини Z, яка є одним з розв’язків
рівняння Z
випадкової величини Z, яка є одним з розв’язків
рівняння Z![]() +2(X/Y)Z–1=0.
+2(X/Y)Z–1=0.
Розв’язання:
1. Знайдемо Z як розв’язання рівняння:
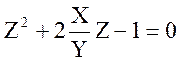 ;
;
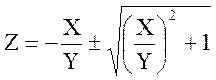 .
.
2. Густина розподілу випадкової величини Z:
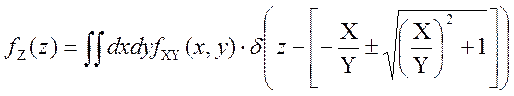 .
.
Відповідь: густина розподілу випадкової величини Z
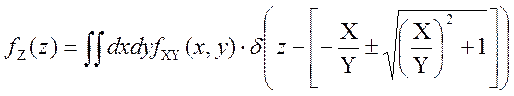 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.