Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 9

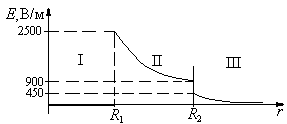
          ОТВЕТ: E₁=0;  

          ЗАДАЧА 7. Заряд Q равномерно распределен по кольцу радиуса R. Найти потенциал относительно бесконечности и напряженность  на оси кольца как функцию расстояния h от центра кольца. Построить графики зависимостей E(h) и φ(h).

ДАНО: Q, Кл  R, м	АНАЛИЗ. Электростатическое поле создано равномерно заряженным кольцом, которое нельзя считать точечным зарядом. Для определения потенциала этого поля воспользуемся принципом суперпозиции электрических
E (h) - ? ;  φ(h) - ?

полей, разбив кольцо на элементарные заряды и определив потенциал поля каждого такого точечного заряда. Суммарный потенциал, очевидно, равен сумме этих потенциалов. При непрерывном распределении зарядов операция суммирования переходит в операцию интегрирования:

Для определения напряженности поля следует воспользоваться связью напряженности и потенциала

                            

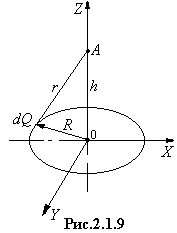
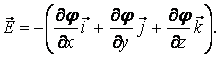
          РЕШЕНИЕ. Разобьём кольцо на элементарные заряды  (рис. 2.1.9).

Потенциал поля, создаваемым каждым элементарным зарядом  в точке А, лежащей на расстоянии h от центра кольца, равен   

       Из  рис.2.1.9 видно, что   Заряд элемента d кольца равен      

. Тогда

 

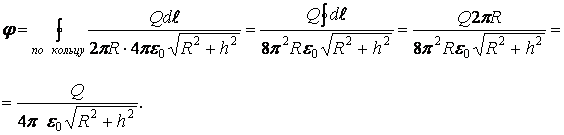
          Проверим размерность: .

Связь напряженности и потенциала дает: ;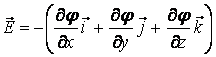

;

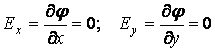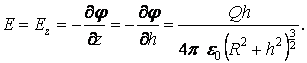
          Проверим размерность: .

Построим зависимость φ(h) (рис.2.1.10).При h=0 (в центре кольца)

, при   .

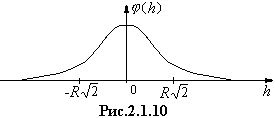
График симметричен относительно оси φ. При .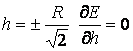

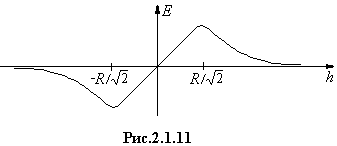
Для φ(h) это точка перегиба. Зависимость E(h) представлена на рисунке 2.1.11. При h=0  E=0; 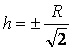–экстремумы функции E(h).

ОТВЕТ: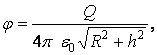  

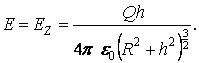
ЗАДАЧА 8. Электрическое поле образовано положительно заряженной бесконечной нитью, с линейной плотностью заряда τ=2×10^-9 Кл/см.  Какую скорость получит электрон под действием этого поля, приблизившись с расстояния r₁=1 см до расстояния r₂=0,5 см от нити.