Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 5

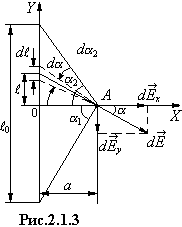
         РЕШЕНИЕ. Спроектируем последнее равенство на координатные оси (рис.2.1.3):

                              

Из рисунка 2.1.3 видно, что

                               (2.1.2)

          При интегрировании по нити будут меняться значения  и r, поэтому все переменные следует выразить через одну - угол  :

                                                                                                           (2.1.3)

Координата у элемента нити  равна :  тогда

                                                         .                                                         (2.1.4)

Подставляя в (2.1.1) выражения (2.1.3) и (2.1.4), получим  .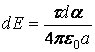

Согласно равенствам (2.1.2),

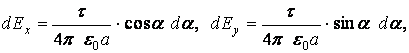
или окончательно

Проверим размерность: .

          Рассмотрим частные случаи, вытекающие из полученных формул:

          1.Точка А расположена на перпендикуляре, проведённом через середину нити, ₁=₂=, тогда

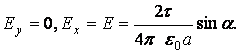
          2.Точка А расположена на перпендикуляре, проведённом к нити через один из её концов, ₁=0 , ₂ =, тогда

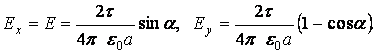
          3. Бесконечная нить,  >>a,  стремиться к ,  стремиться к , тогда   В этом случае силовые линии лежат в плоскостях, перпендикулярных заряженной нити и лучами расходятся от неё. При приближении исследуемой точки А к концам нити будет появляться составляющая

E_у , плоскорадиальная симметрия нарушается.

          ОТВЕТ: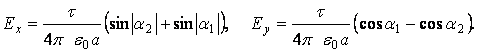

          ЗАДАЧА 4. В вакууме образовалось скопление зарядов в форме тонкого длинного цилиндра с постоянной объёмной плотностью ρ. Найти напряженность поля в точках, лежащих внутри и вне цилиндра.

ДАНО: ρ,  Кл/м3 R, м	АНАЛИЗ. Электростатическое поле образовано бесконечно длинным равномерно заряженным цилиндром.  Симметричное распределение зарядов позволяет применять теорему Гаусса для нахождения вектора . Длина цилиндра   много больше её радиуса
Е-?