Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 7

                                     .                                           (2.1.10)

При вычислении потока вектора напряженности через поверхность S_В следует повторить все рассуждения, которые были проведены для поверхности S_A , тогда

                                                                                              (2.1.11)

Подставим (2.1.10) и (2.1.11) в (2.1.9):  и

где r- текущий радиус.

    Проверим размерность выражения: .

График зависимости E (r) представлен на рис.2.1.5. Для  r =R , E_R=

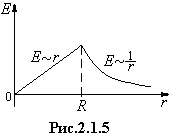
          ОТВЕТ: 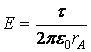  при r>R;   при  r<R..

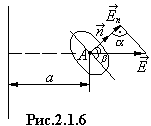
          ЗАДАЧА 5. Электрическое поле созданное тонкой бесконечно длиной нитью, равномерно заряженной с линейной плотностью τ =30 нКл/м. На расстоянии а =20 см от нити находится плоская круглая площадка радиусом r =1 см. Определить поток вектора напряженности через эту площадку, если плоскость её составляет угол β =30⁰ с линией напряженности, проходящей через середину площадки (рис.2.1.6).

ДАНО: τ =30 нКл/м а =0,20 м r =0,01 м β =300	АНАЛИЗ. Электростатическое поле, создаваемое бесконечной заряженной нитью, не является однородным – линии вектора напряженности радиально расходятся от нити, поэтому во всех точках площадки значения и направления вектора  различны. В этом случае поток вектора напряженности через площадку равен интегралу
- ?

где E_n - проекция вектора  на нормаль  к поверхности площадки dS,    – угол между направлением  и нормалью . Тогда

.

          РЕШЕНИЕ. Размеры площадки малы,  r << a, поэтому электрическое поле в пределах площадки можно считать однородным и равным полю в центре площадки:  В этом случае 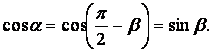  Тогда

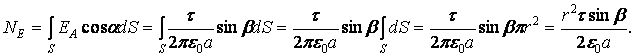
          Проверим размерность:

. Подставим значения

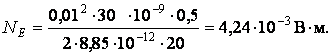
             ОТВЕТ:

          ЗАДАЧА 6. Две концентрические проводящие сферы радиусами R₁=6 см и     R₂= 10 см несут заряды q₁= 1 нКл и q₂=- 0,5 нКл. Найти напряженность E поля в точках, отстоящих от центра сфер на расстояние r₁=5 см , r₂=9 см и