Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 6

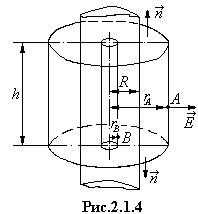
R (цилиндр бесконечно длинный), поэтому в средней части цилиндра силовые линии располагаются радиально, а поле обладает плоскорадиальной симметрией (рис 2.1.4). Вспомогательной Гауссовой поверхности придадим форму цилиндрической, коаксиальной с заряженным цилиндром. Точка, в которой определяется поле, лежит на боковой поверхности вспомогательного цилиндра на расстоянии r_А   то оси цилиндра. Длина вспомогательной цилиндрической поверхности h произвольна, но много меньше длины самого цилиндра, h<<  .

РЕШЕНИЕ. Решим задачу для случая r>R.По теореме Гаусса для поля в вакууме

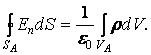                                               (2.1.5)

Поток напряженности через замкнутую цилиндрическую поверхность складывается из потоков через боковую поверхность и через основания вспомогательного цилиндра, поэтому интеграл в равенстве (2.1.5) следует разбить на три интеграла: по боковой поверхности S_бок, верхнему основанию S₁ и нижнему основанию S₂

Поскольку нормаль к основаниям цилиндра составляет угол  с вектором , то

На поверхности S _бок. угол , и

Боковая поверхность вспомогательного цилиндра симметрична относительно заряда, поэтому E= на всей поверхности S_бок. и  Очевидно,  в  результате получим

                                                                               (2.1.6)

Внутри поверхности интегрирования находится заряд, вырезаемый поверхностью  из заряженного цилиндра;  по условию задачи ρ=, поэтому

                                              .                                      (2.1.7)

Подставим выражения (2.1.6) и (2.1.7) в равенство (2.1.5):  откуда

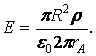                                                                                                          (2.1.8)

Произведение  представляет заряд, приходящийся на единицу длины заряженного цилиндра, т.е. линейную плотность заряда τ: . Следовательно,  формуле (2.1.8) можно придать вид:

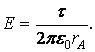
          Проверим размерность: .

          Найдём напряженность поля в точках, лежащих внутри цилиндра при r<R. Вспомогательную поверхность  выбираем в виде цилиндра радиусом r_В и высоты h (r_В<R). По теореме Гаусса

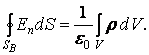                                                                                               (2.1.9)

Внутри поверхности интегрирования находится заряд, вырезаемый поверхностью S из заряженного цилиндра и равный