Электромагнетизм (краткие теоретические сведения и примеры решения задач)

2. ЭЛЕКТРОМАГНЕТИЗМ

2.1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ

2.1.1.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

По закону Кулона сила, действующая между двумя точечными зарядами равна

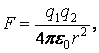
где q₁ и q₂ – электрические заряды тел, r – расстояние между ними,  ε₀ – электрическая постоянная, равная 8,85×10^-12Ф/м.

             Напряжённость и потенциал электрического поля определяются соответственно формулами:

,

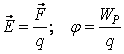где  W_Р  –  потенциальная энергия положительного точечного пробного заряда q.

          Напряжённость и потенциал поля, создаваемого точечным зарядом

E=q/(4π ε₀ r²) ; φ=q/(4π ε₀r),

где r – расстояние от заряда q до точки, в которой определяются напряжённость поля и потенциал.

          Напряжённость и потенциал поля, создаваемые системой зарядов, согласно принципу суперпозиции полей соответственно равны

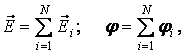
где  и  –  напряжённость и потенциал, создаваемые в данной точке поля

 i-тым  зарядом.

             Напряжённость и потенциал поля точечного диполя с электрическим моментом  находятся по формулам

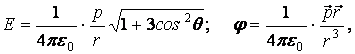
где θ – угол между электрическим моментом диполя   и радиус -вектором , проведенным в точку, для которой ведутся  расчеты.

          Для определения напряженности и потенциала поля, создаваемого  непрерывно распределённым по длине  (площади S, объему V) зарядами Q, выделяется малый заряд dQ, который можно рассматривать как точечный. Напряженность  и потенциал dφ поля, создаваемого зарядом dQ, определяются формулами:

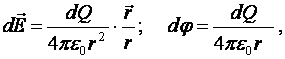
где  - радиус - вектор, направленный от выделенного элемента длины  (площади S, объема V) к точке, в которой вычисляется напряженность.

          Величина заряда dQ определяется по формулам:

          , если заряд распределён равномерно вдоль линии с линейной плотностью τ;

          , если заряд распределён равномерно по поверхности S с поверхностной плотностью ;

          ,  если заряд распределён равномерно в объёме V с объёмной плотностью ρ.

          Напряжённость и потенциал поля, создаваемого непрерывно распределённым зарядом, далее определяется с использованием принципа суперпозиции электрических полей:

          Напряжённость и потенциал поля заряженной сферической поверхности с зарядом  Q  и радиусом  R  равны