Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 8

r₃=15 см. Построить график зависимости E(r).

Из соображений симметрии E₁=E_1n=, следовательно,  Очевидно, , поэтому E₁=0 –напряженность поля во всех точках, удовлетворяющих условию r₁ < R₁ , равна нулю.

          2.Определим напряженность E₂ в области II. Построим вспомогательную сферическую поверхность радиуса r₂. По теореме Гаусса . Из условий симметрии E₂=E_n=, тогда  Ясно, что  поэтому  

Проверим размерность этого выражения:

.

Подставим значения: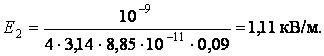

          3.Вычислим напряженность поля в области III. Проведём вспомогательную сферическую поверхность радиуса r₃ .Эта поверхность охватывает заряд

q₁ + q₂ , следовательно, по теореме Гаусса  Учитывая, что E₃=E_n= и  получим:

Правильность формулы по размерности очевидна. Подставим значения:

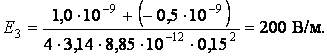
Построим график зависимости E=E (r). При r < R₁ (область I) E₁=0.

В области II  E₂ (r) ~1/r² , в точке  А   r = R₁ ,  E₂(R₁)=q₁ / 4π ε₀R₁² =2500 В/м, в точке  В    r = R₂,  E₂ (R₂)=q₁ / 4π ε₀R₂² =900В/м–слева.

В области III     E₃(r) ~ 1/ r² , причем при r = R₂                справа E₃(R₂)=(q₁+ q₂)/(4π ε₀R₂²) = 450В/м, т.е. в точке r =R₂ функция E(r) терпит разрыв. График функции E=E(r) представлен на рисунке 2.1.8