Электромагнетизм (краткие теоретические сведения и примеры решения задач), страница 2

где Q – заряд сферы.

          Напряжённость поля объёмно – заряженного шара радиуса R равна:

          Напряжённость и потенциал поля, создаваемого бесконечной равномерно заряженной плоскостью, определяется формулами:

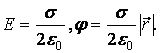
          Напряжённость поля, создаваемого равномерно заряженной бесконечно длинной нитью, равна:

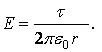
          По теореме Гаусса поток N вектора напряжённости  сквозь любую замкнутую поверхность в вакууме равен суммарному заряду, заключенному внутри этой поверхности, деленному на :

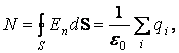
 где ∑q _i – алгебраическая сумма зарядов, находящихся внутри этой поверхности. При помощи теоремы Гаусса можно найти напряжённость электрического поля, создаваемого заряженными телами, если заряд распределён на них симметрично.

          Теорема Гаусса в дифференциальной форме позволяет найти объёмную плотность зарядов ρ(x, y, z) по известной величине напряжённости поля

E(z, y, z), а для одномерного случая – решить и обратную задачу. Теорема Гаусса для вакуума в дифференциальной форме имеет вид:

где - дивергенция вектора , определяемая по формуле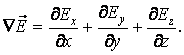

          Для потенциальных полей циркуляция и ротор  равны  нулю. Следовательно, для электростатического поля выполняются условия:

,

где  - ротор вектора,

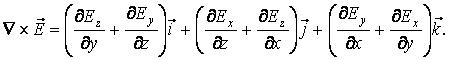
          Связь между напряженностью и потенциалом выражается формулой

где  –градиент потенциала,

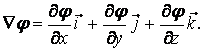
       Уравнение Пуассона связывает потенциал поля с величиной объёмной плотности заряда

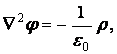
 где 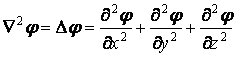  – оператор Лапласа.

          Для поля, обладающего центральной или осевой симметрией,

для однородного поля

где d –расстояние между точками поля с потенциалами φ₁  и φ₂ .

       Работа сил поля по перемещению заряда  q из точки поля с потенциалом  φ₁ в точку с потенциалом  φ₂  равна

А₁₂ =q(φ₁- φ₂).

        Энергия диполя W  во внешнем  электрическом поле и момент  сил, действующих на диполь, соответственно равны:

2.1.2.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

          ЗАДАЧА 1.Два точечных заряда q₁ = -10^-8 Кл и q₂ = 1,5 10^-8 Кл расположены на расстоянии r₁₂ =10 cм друг от друга. Найти силу, действующую на точечный заряд q =10^-9 Кл, помещенный на продолжение прямой r₁₂  на расстоянии