Моделирование и оценивание характеристик сложных систем

II. Моделирование и оценивание характеристик
сложных систем

2. Теоретико-множественное описание сложных систем

2.1. Понятие множества

Определение 2.1. Множеством называется объединение в одно целое некоторой совокупности объектов хорошо различимых нашей интуицией или мыслью.

Множество — это первичное понятие. Поэтому определять его через другие понятия затруднительно. Множества обычно обозначаются большими латинскими буквами.

А, В, С       или   X, Y, Z

Элементы множества обозначают малыми буквами

а, в, с                 или            x, y, z

Запись того, что элемент  x  принадлежит (не принадлежит) множеству  X осуществляется следующим образом:

xÎX   (xÏX).

В теории четких (классических) множеств может быть только две альтернативы:

xÎXлибо (xÏX).

Нечеткое множество задается следующим образом:

X — универсальное множество

A — нечеткое множество; ,

где  – степень принадлежности элемента  x  к нечеткому множеству  A.

Различают следующие виды множеств:

— конечные                        счетные

— бесконечные

                                            несчетные

Определение 2.2. Конечное множество — это множество, состоящее из конечного числа элементов (может быть и число, и объект).

Определение 2.3. Бесконечное счетное множество — это множество, элементы которого могут быть взаимно однозначно сопоставлены элементам множества натуральных чисел.

Определение 2.4. Бесконечное несчетное множество — это такое множество элементов, которым нельзя сопоставить множество натуральных чисел.

Существуют 2 способа задания множеств:

— прямое перечисление элементов, входящих в множество (для конечных множеств);

— задание некоторых свойств, которым удовлетворяют элементы множества.

Примеры.                  

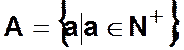
Правил транзитивного высказывания

Пример:                     

                                    , т.к. в эти множества входят одни и те же элементы.

Определение 2.8. Объединением двух множеств X, Y назовем такое множество D, для которого выполняются следующие условия.

Определение 2.9. Пересечением двух множество X и Y назовем такое множество D₂, для которого выполняются следующие условия.

Определение 2.10. Разностью двух множеств X и Y назовем такое множество D₃, для которого выполняются следующие условия.

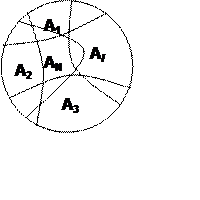Определение 2.11. Покрытием множества  назовем семейство множеств, для которого выполняется следующее условие.

Основные операции, применяемые к множествам и их элементам:

 — объединение множеств;

 — пересечение множеств;

\ — взятие разности множеств;

 — дизъюнкция (или);

 —конъюнкция (и);

 — квантор всеобщности (для всех);

 — квантор существования (существует);

 — импликация (следует);

 — эквивалентность (тогда и только тогда);

 — отрицание (не).

card X — мощность множества.

Для конечных множеств card B(X)=2ⁿ, где n — число элементов множества .

 — пустое множество (множество, не содержащее ни одного элемента .

2.2. Основные операции над множествами.

Определение 2.5. Множество Y называется подмножеством (частью) множества X, если оно содержит только элементы, входящие в множество X.

 — символ включения одного множества в другое,

 — символ, обозначающий ситуации, когда одно множество является собственным подмножеством другого множества.

Определение 2.6. Множество Z называется собственным подмножеством (правильной частью) множества X, если выполняются следующие условия

.

Определение 2.7. Множества Y и X равны тогда и только тогда, когда выполняются следующие соотношения

.

Определение 2.12. Разбиением множества  назовем семейство множеств, для которого выполняется следующее условие

           ,      

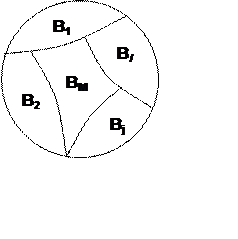
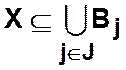
Примеры. Дано ; 

Определение 2.13. Булеаном множества X называется множество, состоящее из всех подмножеств данного множества, включая само множество и пустое множество

B(X)

2.3. Кортежи и декартовые произведения множеств.

Определение 2.14. Кортежем будем называть упорядоченное множество элементов

 — кортеж длины n

Определение 2.15. Декартовым (прямым) произведением n — множеств вида  называется множество таких всевозможных кортежей длины “n”, для которых первый элемент кортежа , второй элемент кортежа  и т.д.

Замечание. Декартова плоскость, декартово произведение — частные случаи декартова произведения.

Определение 2.16. Если , то в этом случае декартово произведение этих множеств называется декартовым произведением или декартовой n–ой степенью ().

Примеры:          , 

                           ;  

2.4. Определение  отношения.

Определение 2.17.n-арным отношением называется основная математическая конструкция, записываемая в следующем виде:

,

где    — базисные множества, на которых задается отношение,