Моделирование и оценивание характеристик сложных систем, страница 7

p1   p2   p3   p4   t2   t1

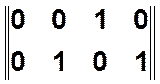
         Нахождение маркера в соответствующей позиции сети Петри интерпретируется следующим образом:

 — задание находится в состоянии ожидания,

 — процессор находится в состоянии ожидания,

 — задание выполняется процессором,

 — задание выполнено и ожидает вывода,

 — начало выполнения задания,

 — конец выполнения задания.

Определение 3.5.  Маркированной сетью Петри общего вида называется пятерка следующего вида

где  — конечное множество позиций,

 — конечное множество переходов

 и  — графики бинарных отношений, заданных на множестве  и мультимножестве  с неограниченных тиражированием.

,      

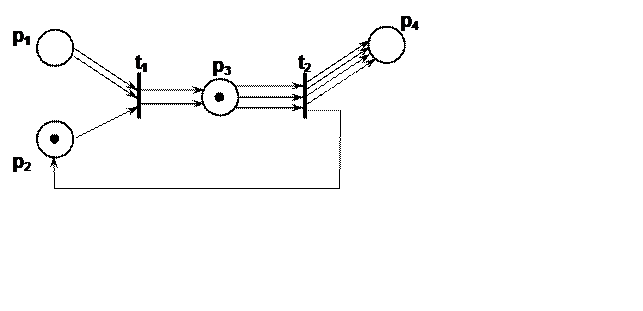
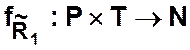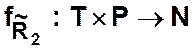
Принципы функционирования сети Петри

         В основе функционирования сети Петри лежит процесс изменения ее маркировки (переход из одного состояния в другое). В случае запуска (срабатывания) соответствующих переходов, конструктивно правило функционирования сети Петри задается с помощью:

-  правил разрешения переходов,

-  правил изменения состояний маркировки при запуске (срабатывании) перехода.

Правило разрешения перехода.

         Переход  разрешен, если каждый его входной дуге (ребру)  может быть поставлен в соответствие по крайней мере один маркер (фишка) в позиции, из которой данная дуга исходит. Это правило может быть записано следующим образом

.

Существует эквивалентная запись в векторно-матричной форме

.

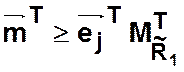где 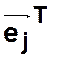 — вектор-строка, которая имеет число элементов, равное числу переходов, из них –й равен 1, а остальные — нулевые.

Правило изменения состояния маркировки.

         При запуске перехода  из каждой его входной позиции  должно быть изъято число маркеров (фишек) равное кратности ребер, соединяющих позицию  и переход , и в каждую его выходную позицию  должно быть дополнительно помещено к уже имеющимся маркерам число маркеров (фишек) равное кратности ребер, соединяющих переход  с позицией .

Данное правило записывается в эквивалентной векторно-матричной форме следующим образом:

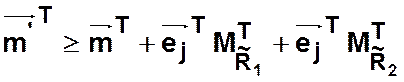
Пример

 

     ,                  ,            

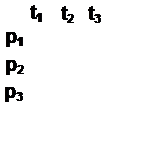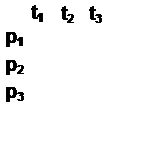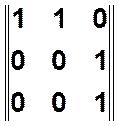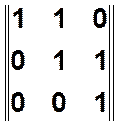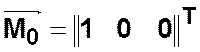
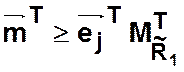
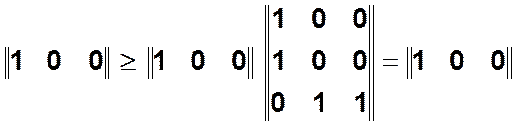 — переход  может сработать.

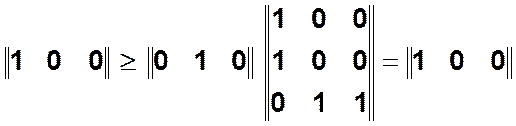 — переход  может сработать.

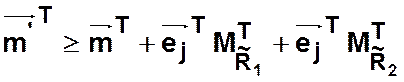
         Пусть сработал переход .

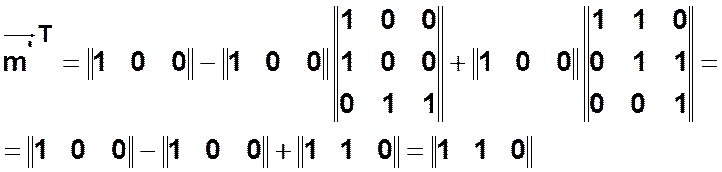
         Пусть сработал переход .

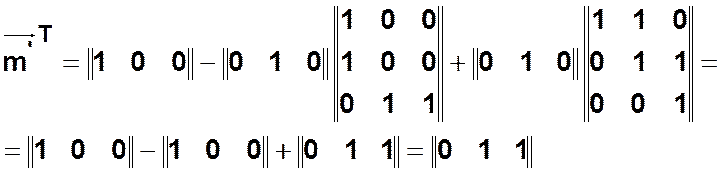
Построение деревьев достижимости

         Основные методы анализа сети Петри базируются на построении и исследовании деревьев достижимости для соответствующих сетей Петри. Суть процедуры построения состоит в следующем. В качестве корня дерева принимается вершина графа, соответствующая начальной маркировке сети Петри. Далее выявляются все разрешенные при этой маркировке переходы и определяются получаемые при их запуске маркировки, каждой из которых сопоставляется вершина дерева, непосредственно достижимая из начальной. Затем та же процедура повторяется для каждой из этих вершин и т.д.

Тупиковые вершины — это вершины, из которых уже нельзя осуществлять никакие переходы.

Дублирующие вершины — это вершины, в которых повторяется маркировка.

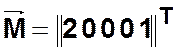 — корневая или начальная вершина.

4. Основы структурного анализа сложных
объектов и систем.

4.1. Основные понятия и определения.