Моделирование и оценивание характеристик сложных систем, страница 6

                       (3)

                       (4)

         Будем рассматривать детерминированные КА (возмущающее воздействие отсутствует ). Тогда

, ,  — конечные множества.

         Функционирование КА интерпретируется как переходы КА из состояния в состояние, которые происходят в дискретные моменты времени (такты) , имеющие нумерацию . В этом случае, базисное множество  представляется в виде счетного множества вида .

         КА является ДС со счетным множеством моментов времени и относится к классу ДС с дискретным временем. Если интервалы между последовательными тактами равны, говорят о синхронной конечной ДС, в противном случае об асинхронной.

                                  (5)

                                  (6)

         Из анализа выражений (2.9.5) следует, что переходная функция  сопоставляет каждой паре символов  (<состояние предыдущего такта, текущий вход>) символ текущего состояния

автомат 1 рода 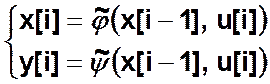     —  несдвинутая выходная ф-ция

автомат 2 рода 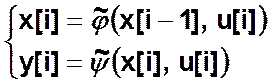      —  сдвинутая выходная ф-ция

         Возможен вариант задания автомата, когда выходная функция имеет вид:

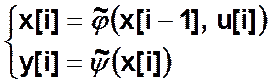 — автомат типа «вход–выход» или автомат Мура
2-го рода.

         Иногда при определении автомата рассматривают не пятерку , а шестерку , где  — начальное состояние автомата.

         Наиболее часто встречаются 5 основных способа задания КА:

-  задание КА табличный способ задания КА,

-  задание КА с помощью орпсевдографов,

-  задание КА с помощью специальных булевых матриц,

-  задание КА с помощью специальных грамматик,

-  задание КА с помощью рекуррентных отношений.

Пример. Рассмотрим конечный автомат (КА) Мура.

,   ,  

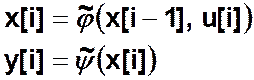
а) Табличный способ задания КА.

Вход Состояние

б) Графический способ задания КА. Орпсевдограф (допускается наличие петель в вершинах графа и множественность ребер).

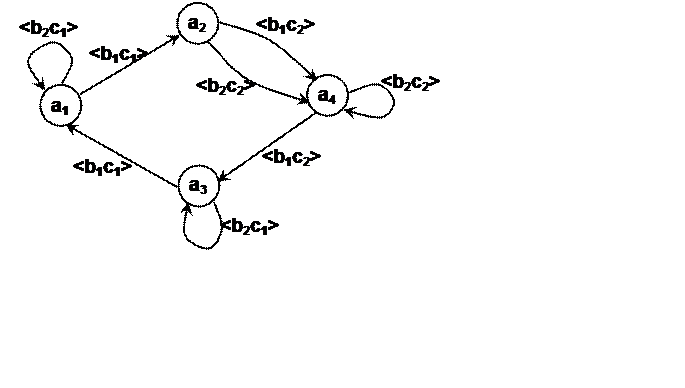
в) Матричный вариант задания КА (используются специальные булевые матрицы).

Число строк и столбцов матрицы соответствует количеству состояний КА.

Состоянию  отвечает вектор-строка 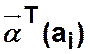, в которой все элементы нулевые, кроме элемента, соответствующего  и принимающего значение равное единице.

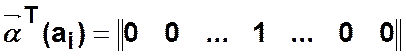
Например,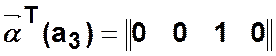

         Выходному элементу  соответствует булева вектор-строка вида:

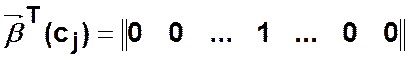
Введенное представление позволяет рассчитать матричными методами выход КА при любом начальном состоянии и любой последовательности входных воздействий.

Пример.

Дано 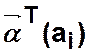 — начальное состояние КА,
 — сценарий задания входного воздействие (2 такта).

Найти  .

Переходное состояние автомата определяется по формуле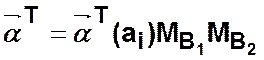

Тогда выход автомата определится по следующей формуле

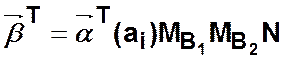
3.3. Сети Петри — причинно-следственные динамические модели параллельных действий.

Определение 3.4.  Ординарной маркированной сетью Петри называется пятерка следующего вида

где  — конечное множество позиций ,

 — конечное множество переходов ,

 и  — графики бинарных отношений, заданных на множествах  и :  и .

 — вектор начальной маркировки ,  .

         Геометрически сеть Петри задается двудольным графом, который конструктивно задается с помощью двух бинарных отношений  и :

1.   задает связь входных позиций с переходом,

2.   задает связь выходных позиций с переходом.

Маркер (фишка) геометрически задается как  и располагается в заданной позиции.

Существуют взаимно однозначные соответствия между графиками отношений  и  и представлением структуры сети Петри с помощью входной и выходной функций инцидентности  и :

,  

Данные функции, в свою очередь, описываются матрицами инцидентности  и  рассматриваемых отношений и графа.

Пример.  Пусть с помощью сети Петри мы описываем процесс функционирования вычислительной системы (ВС). Тогда структура ВС задается с помощью  и :