Моделирование и оценивание характеристик сложных систем, страница 5

Пример. ,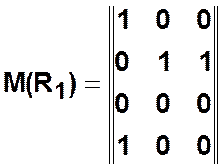  

;   ; 

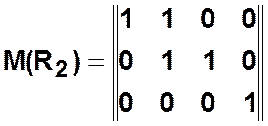
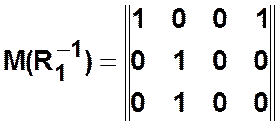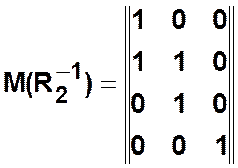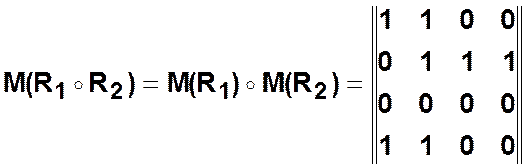
3. Примеры теоретико-множественного описания сложных систем

3.1. Сетевые модели сложных систем (СМСС).

СМСС задаются следующим образом

Пример.

3.2. Динамические модели сложных систем

Определение 3.1.  Статическая модель описывает связь между компонентами состояний или между этими компонентами и другими характеристиками системы в условиях равновесия и других условиях «замораживания» изменения состояния.

Определение 3.2.  Динамической называется модель, в которой в той или иной форме раскрываются причинно-следственные связи (реализуется принцип причинности), определяющие развивающийся во времени процесс перехода системы из одного состояния в другое.

Принцип причинности предполагает выполнение следующих условий:

a)  упорядоченность причинно-следственных связей во времени. Это означает, что состояние и выходная ситуация (выход) системы в любой момент времени не зависит от ситуаций, которые могут возникнуть на входном полюсе системы в более поздние моменты времени.

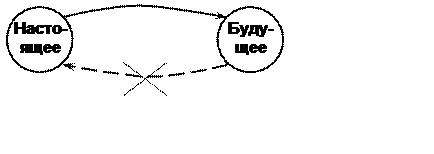
b)  однозначность причинно-следственных связей. Это означает, что состояние и выходная ситуация (выход) системы в любой момент времени в будущем может быть определена совершенно точно (однозначно), если точно известны:

o  все сведения о системе, характеризующие ее, и воздействие на нее среды в прошлом и настоящем;

o  входное воздействие на систему в будущем.

Первая часть этого принципа (пункт а) эквивалента утверждению о том, что будущее системы не влияет на прошлое и констатирует необратимость явлений во времени. Вторая часть данного принципа (пункт b) отражает принципиальную познаваемость причинно-следственных связей в системе и возможность точного предсказания выхода системы при наличии необходимой информации.

Таким образом, система, удовлетворяющая принципу причинности, является динамической системой.

Определение 3.3.  Кинематической моделью называется модель динамической системы, описывающая изменение состояния как функции времени и не раскрывающая причинно-следственные связи, вызывающие это изменение.

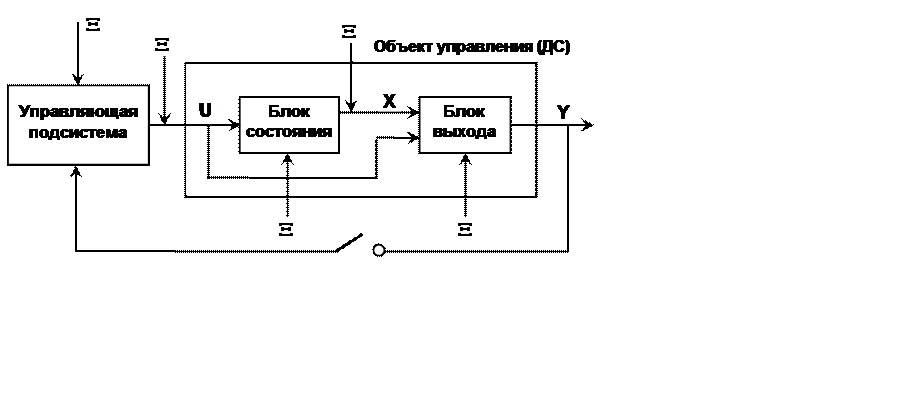
Динамическая система (ДС) задается с использованием 4-х основных (базисных) множеств:  и 2-х отображений: . При этом

 — множество состояний ДС,

 — множество выходов ДС,

 — множество управляющих воздействий,

 — множество возмущающих воздействий,

 — множество моментов времени,

 — множество входных воздействий,

 — переходное отображение,                 (1)

 — выходное отображение,                    (2)

Переходное и выходное отображения задаются как функции
 и .

 — классическая ДС.

         При этом каждое из множеств  может быть в свою очередь конечным, счетным, континуальным, превышающим мощность континуума; множество  может быть континуальным и дискретным (счетным либо конечным).

         Обобщенное описание ДС позволяет, анализируя свойства множеств и отображений:

-  образовывать различные конкретные частные классы моделей ДС;

-  устанавливать взаимосвязи между указанными классами;

-  организовывать многомодельные исследования реально протекающих процессов.

Основные классы задач теории управления ДС (ТУ ДС) (детерминированный вариант задания исходных данных)

Элементы ДС Классы задач ТУ ДС	U	X	Y
Задачи  анализа	+	+	?
Задачи наблюдения (мониторинга)	+	?	+
Задачи управления	?	+	+

Пример. Конечномерные дифференциальные динамические системы (КДДС).

, ,  — представляет собой конечномерные пространства,

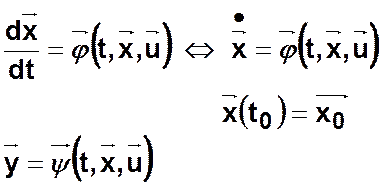
Нестационарная линейная ДДС (НЛДДС)

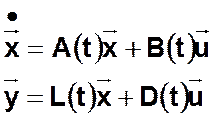
Стационарная линейная ДДС (СЛДДС)

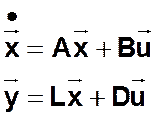
Билинейная КДДС

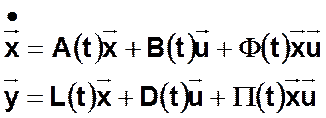
Рассмотрим частный случай ДС — конечные автоматы (КА) (конечные ДС).

В общем случае КА задаются на 3-х основных множествах с использованием 2-х отображений вида: