Моделирование и оценивание характеристик сложных систем, страница 2

 — график отношения, представляющий собой некоторое подмножество декартова произведения базисных множеств  (из всевозможных вариантов сочетаний множеств выбираем определенное сочетание, которое уже является описанием конкретной системы).

*  Для описания реально функционирующих систем используют, как правило, не одно, а несколько отношений.

*  Отношения в зависимости от «арности» бывают унарные (n=1), бинарные (n=2), тернарные (n=3), кватернарным (n=4) и т.д., а в общем случае   n–арные.

*  В частном случае множества, на которых строится n–арное отношение, могут быть равными , и соответственно декартово произведение этих множеств представляет собой декартову n–ю степень .

Определение 2.18.  Конструкция вида , где  — некоторое базисное множество отношения, n — число, определяющее арность отношения, а  — график отношения называется n–арным (n-местным) отношением, заданным на множестве .

Примеры:   а)  — множество объектов городского хозяйства,  — множество объектов городского хозяйства, которые подвергаются инвентаризации.      — унарное отношение

б)  — множество студентов,  — множество преподавателей,  — множество пар вида <студент, преподаватель>. Тогда  — бинарное отношение, заданное на  и , которое определяет порядок закрепления студентов за преподавателями.

в)   — множество должностных лиц (элементов производства, компонент информационно-вычислительных средств), а  — подмножество пар лиц (элементов производства, компонент информационно-вычислительных средств), между которыми возможен (допустим) обмен информацией. Тогда  — бинарное отношение, заданное на , описывающее возможности обмена информацией между элементами .

г)  — множество вещественных чисел,  — подмножество точек n–мерного пространства. В этом случае n–арное отношение  — может описывать совокупность точек n–мерного пространства, обладающих теми или иными свойствами, например, принадлежность некоторой произвольной кривой, поверхности, фигуре.

2.5. Формы представления бинарных отношений.

         В соответствии со сформулированным выше общим определением бинарное отношение записывается в виде , где ,  — множества, на которых задается отношение, а  — график отношения. Если пара  удовлетворяет отношению  и, следовательно, является элементом графика , вводятся следующие записи:  или .

Частные случаи задания бинарного отношения:

а) случай полного отношения — ;

б) случай пустого отношения — .

         Пусть  и  — конечные множества , . Тогда  будет включать в себя  пар элементов. В общем случае бинарное отношение  будет включать меньшее число пар, и выделение этих пар будет базироваться на заданной содержательной интерпретации той или иной прикладной задачи.

Пример:  — множество объектов городского хозяйства,
 — множество сотрудников проектно-инвентаризационных бюро (ПИБ), входящих в состав ГУИОН,  — отношение, характеризующее порядок выделения сотрудников ПИБа на инвентаризацию объектов городского хозяйства.

         Существует несколько способов задания бинарных отношений:

а) Прямое перечисление пар, удовлетворяющих бинарному отношению:

;   

б) Представление с помощью решеток с узлами.

 

в) Представление бинарных отношений с помощью булевой матрицы , m-строк, n-столбцов.

 

   

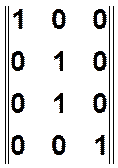
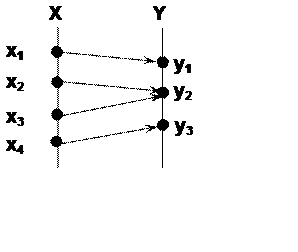г) Стрелочное представление бинарных отношений.

д) В случае, если множество  и  — бесконечные, то  может задаваться в виде аналитических выражений.

;  

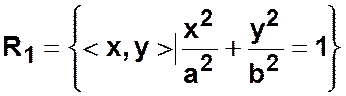 — эллипс на плоскости

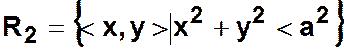 — множество точек окружности радиуса   а.

2.6. Проекции и сечения бинарных отношений. Определенность (неопределенность) и однозначность (многозначность) бинарных отношений.