Моделирование и оценивание характеристик сложных систем, страница 8

Определение 4.1.  Структурный анализ — научное направление, имеющее своей целью исследование таких основных характеристик структур сложных систем, как связность, компактность, достижимость, сложность, иерархичность, централизованность (децентрализованность).

Ориентированный маршрут (ормаршрут) — это такая последовательность ребер (дуг) ориентированного графа (орграфа), для которой начало каждой дуги совпадает с концом предшествующей.

Путь — ормаршрут, в котором нет повторяющихся дуг и отсутствует совпадение начальной и конечной вершин.

Простой путь — путь, в котором нет повторяющихся вершин.

Длина пути  — число дуг орграфа.

Ориентированный граф называется связным, если для любых двух его различных вершин существует, по крайней мере, один путь, их соединяющий.

Контур — путь, в котором начало первой дуги совпадает с концом последней.

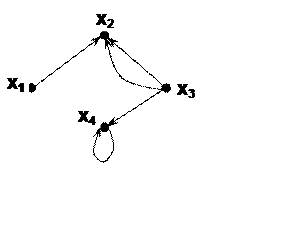
Рис. 4.1.

Этот орграф соответствует бинарному отношению следующего вида:

,

,   ,

, где

 — множество вершин графа,

 — множество ориентированных ребер или дуг графа, обозначаемых соответственно .

Матрица смежности  представляет собой квадратную матрицу, каждый элемент  которой

-  принимает значение , если вершина  непосредственно связана с вершиной  ориентированным ребром;

-  принимает значение  — в противоположном случае.

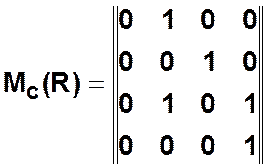
 — полустепень исхода вершины . Количество дуг, выходящих из вершины . Ей соответствует число единиц -й строки данной матрицы.

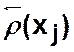 — полустепень захода вершины . Количество дуг, входящих в вершины . Ей соответствует число единиц -го столбца данной матрицы.

Вершины, для которых  называются стоками.

Вершины, для которых 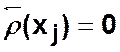 называются истоками.

В матрице инцидентности  ориентированного графа

-  каждая –я строка соответствует дуге (ориентированному ребру) ,

-  каждый –й столбец соответствует вершине .

Рис. 4.2.

В матрице  орграфа, представленного на рис.4.2,

-  элемент  принимает значение , если вершина  не инцидентна дуге ,

-  элемент  принимает значение , если дуга  выходит из вершины ,

-  элемент  принимает значение , если эта дуга входит в вершину .

   

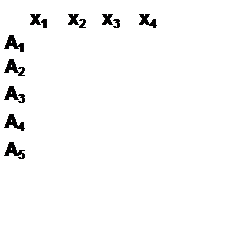
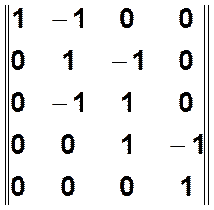
Степенные матрицы 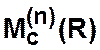 — матрицы, характеризующие бинарные отношения, получаемые при проведении –раз последовательной композиции матрицы смежности.

,   ,    ,    

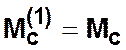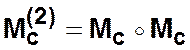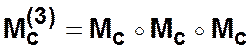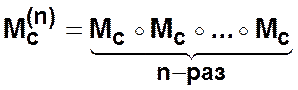
Если в матрице 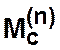 элемент , тогда существует хотя бы один путь длины  из  в , который может содержать повторяющиеся вершины. Если же при этом выполняется соотношение

,

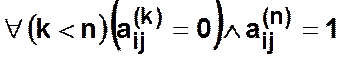то  есть наименьшая длина пути из  в .

Если , то 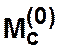 называется единичной матрицей

.

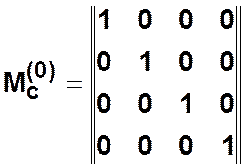Операция транзитивного замыкания бинарного отношения

Пусть задано бинарное отношение следующего вида:

Проведем –раз последовательную композицию

   

………………………………………….

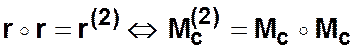
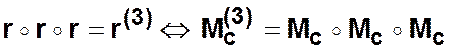
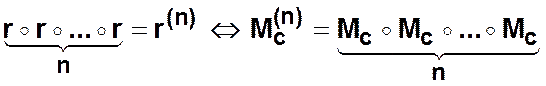
         Тогда отношение транзитивного замыкания  записывается в следующем виде

         В этом случае матрица отношения транзитивного замыкания  определится следующим образом:

.

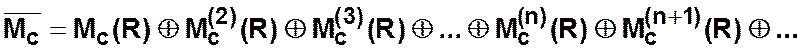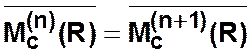 — критерий окончания транзитивного замыкания.

Пример.  Пусть топологическая структура наземного комплекса управления (НКУ) космическими аппаратами (КА) задана с помощью орграфа, представленного на рис. 4.3.

Рис. 4.3.

 — множество элементов НКУ, где

 — центр управления полетом КА,

 — командно-измерительные комплексы.

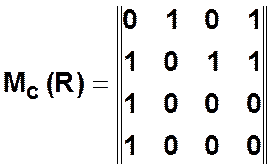 — матрица смежности, которая задает возможные варианты взаимосвязей элементов НКУ.

Решение путем транзитивного замыкания.

1 шаг.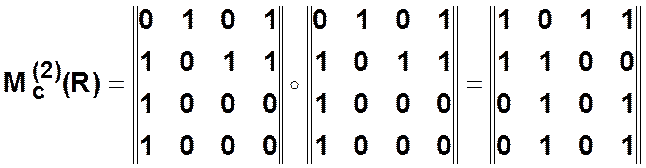

2 шаг.

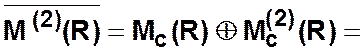
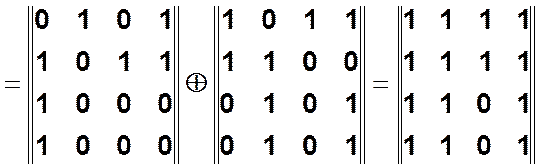
3 шаг.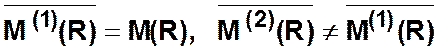

4 шаг.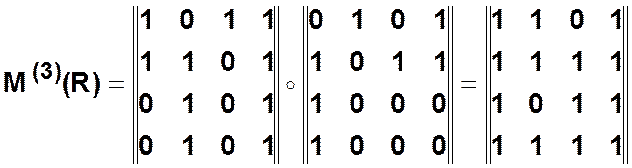

5 шаг.

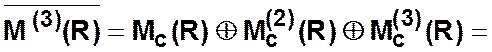
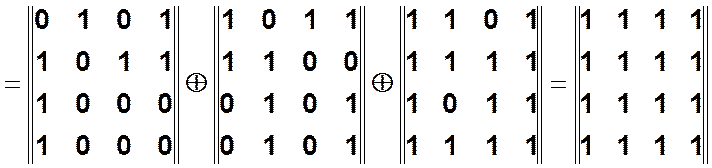
6 шаг.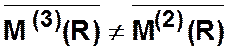

7 шаг.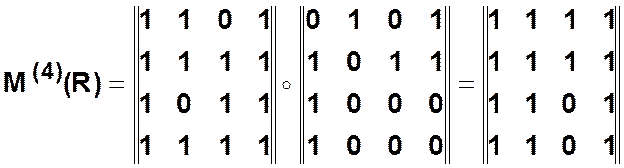

8 шаг.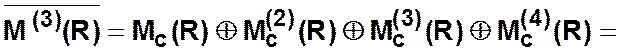

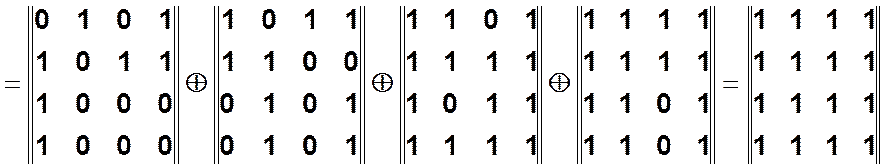
9 шаг.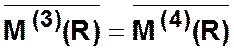

Рис. 4.4.

Матрица достижимости  — матрица транзитивного замыкания с добавлением единичной матрицы.

         В матрице достижимости  элементы могут принимать следующие значения:

-  если элемент 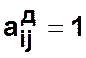, то это означает, что существует хотя бы один маршрут (путь) длины от  до  из вершины  в вершину ;

-  если элемент 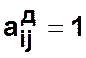 и 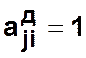, то это означает что вершины  и  сильно связаны;

-  если элемент 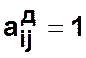 или 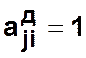, то мы имеет односторонние связанные вершины;