Моделирование и оценивание характеристик сложных систем, страница 4

Определение 2.27.  Всюду определенное слева и однозначное слева бинарное отношение  называется отображением или функцией

Для отображения используются специальные формы записи:

;

Определение 2.28.  Левое сечение графика  по элементу  называется образом элемента  в

.

Определение 2.29.  Правое сечение графика  по элементу  называется прообразом элемента  в

.

Определение 2.30.  Не всюду определенное слева и однозначное слева бинарное отношение  называется частичным отображением (частичной функцией).

 

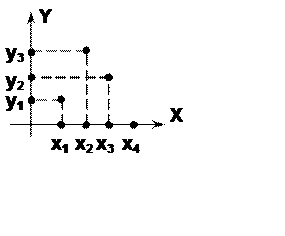Определение 2.31.  Бинарное отношение  всюду определенное слева и многозначное слева называется мультиотображением.

 

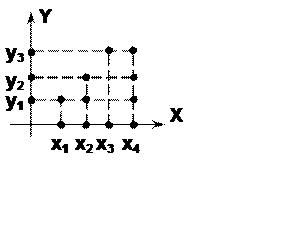Определение 2.32.  Бинарное отношение  не всюду определенное слева и многозначное слева называется частичным мультиотображением (частичной многозначной функцией).

 

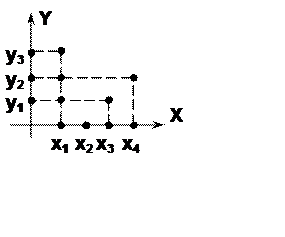         Способы описания отображений, заданных на двух множествах такие же, что и для бинарных отношений:

-  непосредственное перечисление пар,

-  стрелочное представление,

-  матричное представление,

-  представление с помощью решетки.

         Основные классы отображений

а) ,  — конечные множества
б)  — множество вещественных чисел,  — множество вещественных чисел
в) ,     (,  отображение из 2-х мерного пространство в одномерное пространство , )

2.8. Операции над бинарными отношениями.

         Графики отношений являются множествами, поэтому над ними можно производить также ранее введенные теоретико-множественные операции, как операции объединения, пересечения, взятия  разности.

         В отличие от обычных множеств для графиков бинарных отношений вводятся операции инверсии   и    композиции.

         Рассмотрим все перечисленные операции

         Пусть ,  — бинарные отношения, заданные на m–элементном множестве  и n–элементном множестве , а ;  — булевы матрицы типа , представляющие эти отношения. В результате объединения, пересечения и взятия разности графиков  и  определяются бинарные отношения , ,    .

         Для нахождения соответствующих матриц, представляющих графики указанных отношений, используются следующие процедуры:

-  «объединение» матриц      — почленное суммирование  соответствующих элементов по правилу булева сложения   0+0=0,   0+1=1,   1+0=1,   1+1=1;

-  «пересечение» матриц        — почленное умножение  по правилу булева умножения    0´0=0,   0´1=0,   1´0=0,   1´1=1;

-  «взятие» разности матриц  y  —
почленное вычитание по правилу     0–0=0,   0–1=0,   1–0=1,   1–1=0.

Пример.   ,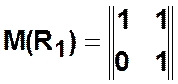  

,   ,   .

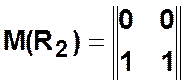
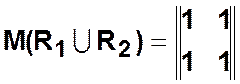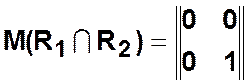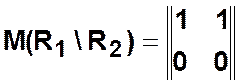Определение 2.33.  Инверсией бинарного отношения , заданного на множестве , , называется операция построения обратного к  отношения следующего вида , заданного на , , график которого удовлетворяет условию .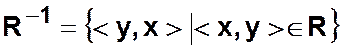

         Таким образом, операция инверсии сводится к замене каждой пары  инверсной парой . Если отношение  представлено матрицей , то отношение  представляется транспонированной матрицей .

Определение 2.34.  Композицией бинарных отношений ,  называется такое отношение , график которого удовлетворяет следующему условию .

         Таким образом, операция композиции бинарных отношений  и  определена тогда и только тогда, когда правое множество первого отношения и левое множество второго отношения совпадают. Множество прибытия первого отношения совпадает с множеством отправления второго отношения.

         Если элемент  связан с элементом , то это будем записывать впредь следующим образом .

         Если ,  конечны и графики ,  заданы булевыми матрицами , , то композиция отношений  и  соответствует произведение указанных матриц

.

         Перемножение осуществляется по правилам перемножения матриц, но при действиях над элементами используются приведенные выше правила булева сложения и умножения.