Моделирование и оценивание характеристик сложных систем, страница 9

-  если для  и для  выполняется следующая пара условий 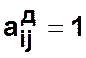, , 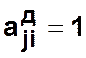то говорят, что орграф является сильно связным;

-  если для  и для  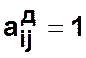, то говорят, что орграф является односторонне связным.

Матрица расстояний . Если заменить в матрице достижимости каждую единицу длиной соответствующего кратчайшего пути (для диагональных элементов этот путь будет иметь длину ноль), а каждый не диагональный нуль заменим на  (или каким-либо большим положительным числом), то получим матрицу расстояний.

Пример.

,              

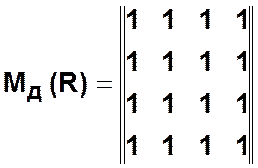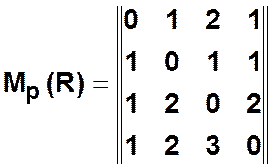
4.2. Показатели (характеристики) количественного оценивающие структуры сложных систем (СлС).

4.2.1. Показатель  связности структуры СлС.

Показатель связности структуры  для –вершинного графа определяется как отношение суммарного числа ребер к минимальному их числу, при котором может быть построен связный граф с  вершинами (величина ). Для ориентированного графа показатель связности  может быть определен как отношение суммы полустепеней исхода (или захода) вершин, равной сумме элементов матрицы смежности  к величине .

Показатель связности для ориентированного графа:

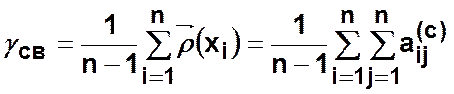
Показатель связности для неориентированного графа:

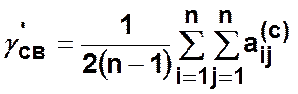
 — показатель избыточности.

Пример. Для приведенного на рис. 4.4 графа () показатель связности 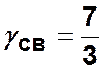, а показатель избыточности .

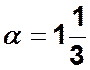4.2.2. Показатель  достижимости структуры СлС.

         Коэффициент достижимости  определяется для ориентированных графов как отношение суммы всех элементов матрицы достижимости  к :

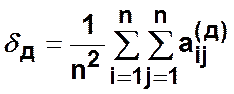
Пример. Для графа, изображенного на рис.4.4, . Если на этом графе удалить вершину , то имеем следующую структуру:

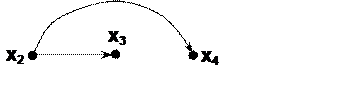
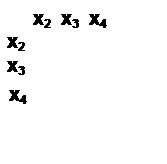В этом случае получаем матрицу достижимости следующего вида

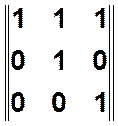    и имеем .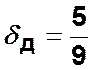

4.2.3. Показатели  компактности  структуры СлС.

Данные показатели определяются на основе матрицы расстояний .

Эксцентриситеты вершины графа  — это наибольшее из кратчайших расстояний от вершины  до других вершин графа . Для каждой вершины графа  эксцентриситет равен

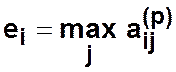
Радиус  — наименьший из эксцентриситетов графа

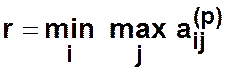
Диаметр  — наибольший из эксцентриситетов графа

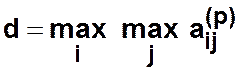
Центральная вершина графа — это та его вершина , для которой выполняется следующее условие

Центр графа — множество центральных вершин.

Чем  и  меньше, тем структура компактнее.

Пример. Из матрицы расстояний 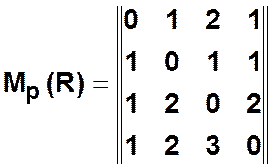 получаем 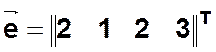, , . Центр состоит только из одной центральной вершины .

Интегральный показатель структурной компактности определяется как сумма всех элементов матрицы расстояний  (чем меньше этот показатель, тем структура компактнее)

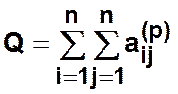
Для полного графа .

Относительный показатель компактности

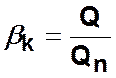
Пример. Для графа рис. 4.4  , ,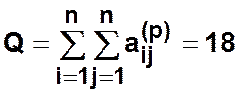

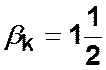
4.2.4. Показатель  централизованности  структуры СлС.

Данный показатель определяется следующим образом: для каждой вершины матрицы смежности  подсчитывается суммарное число входящих и выходящих дуг (полустепеней захода и исхода)

Находят наибольшее из них ,определяют разность между  и  и суммируют эти разности. Максимально возможное значение этой суммы будет . Тогда индекс централизованности определится следующим соотношением:

.

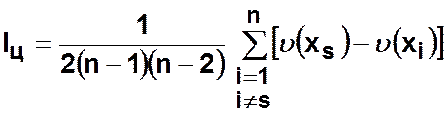Пример. Для рассматриваемого графа (рис. 4.4) , , , . Следовательно , , , . Таким образом, .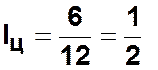

Примеры типовых структур современных
телекоммуникационных систем.

Цепь	Круг
Полный граф	Штурвал

Выводы. Зная показатели (характеристики), оценивающие структуры СлС, мы можем при проектировании или эксплуатации соответствующих информационных систем говорить о тех или иных свойствах данных систем. Так, например,

-  если система имеет высокую степень связности, большую избыточность и равномерные распределения связи, то она обладает высокой надежностью;

-  если система имеет минимальный показатель компактности, то это обуславливает высокое быстродействие системы;

-  если степень централизованности мала, то имеем распределенную структуру, обладающую высокой степенью живучести.