Автоматизированные системы управления технологическими процессами: Методические указания к лабораторным работам и домашним заданиям, страница 7

Таким образом, находят последовательность функций или табличных соответствий:

U^*[N-1] = U(x [N-1]),        ü

U^*[N-2] = U(x [N-2]),        î                                                (7)     

................................         ì      N – оптимальных управлений на

U^*[N-K] = U(x [0]).           þ             каждом шаге    

Так как в последнем соотношении x[0] задано - это начальная точка траектории, то из выражения (4) получим

x^*[1] = x[0]+j(x[0],U^*[0]),       (8)

                         x^*[2] = x[1]^*+..................

В конечном итоге получатся оптимальные x^*[k], U^*[k].

                                   3. Содержание работы

В работе необходимо ознакомиться с применением метода динамического программирования для задач оптимизации поведения непрерывного инерционного объекта под воздействием некоторого управления. Решение проводится численным методом. При решении задачи нужно находить экстремум функции одной переменной произвольным известным методом.

                     4. Порядок выполнения работы

4.1. Изучить постановку задачи, метод ее решения, переход  к дискретному представлению исходных уравнений.

4.2. Изучить аналитический метод решения поставленной задачи [2].

4.3. Составить уравнения решения для заданного объекта j, функционала потерь Q в области допустимых управлений V .

4.4. Изучить алгоритм дискретного многошагового процесса оптимизации [1].

    4.5. Разработать алгоритм решения задачи динамического программирования для заданного объекта. Провести дискретизацию диапазона изменения управления и координат состояния. Значения DU и Dx выбрать из соображений достаточной точности результата. Считать попадание траектории движения объекта в диапазон Dx как попадание в точку начала данного диапазона.

4.6. Написать программу и получить результат оптимального управления, и траекторию движения объекта на заданном интервале времени.

4.7. Проверить полученное решение на оптимальность.

5. Содержание отчета

5.1. Цель работы. Постановка задачи, основные исходные данные.

5.2. Дискретные уравнения, полученные из заданных непрерывных выражений для объекта, функционала, рекуррентное соотношение процесса оптимизации.

5.3. Аналитическое решение задачи для 4-шагового процесса оптимизации.

5.4. Графическое построение хода решения задачи.

5.5. Алгоритм процесса оптимизации, разработанный для поставленной задачи.

5.6. Программа, реализующая разработанный алгоритм.

5.7. Результаты аналитического расчета, вычислений на ЭВМ и проверки на оптимальность полученного решения.

5.8. Выводы.

                           6. Исходные данные

6.1. Уравнение движения объекта

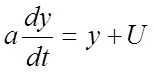       ,    y(0) = 0, y(N) = 1                    (9)

6.2. Функционал потерь

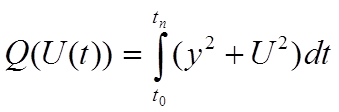                                 (10)

6.3. Ограничение на управление

        |U(t)|U_m

6.4. Величины a, U_m, t₀, t_n , N задаются преподавателем.

6.5. Величины Dy , DU выбираются самостоятельно из

соображений разумной точности результата.

                       7. Контрольные вопросы

7.1. Принципы, эаложенные в методе динамического программиpования. Графическая интерпретация метода.

7.2. Дискpетный метод решения оптимизационной задачи.

7.3. Применимость метода для решения вариационных задач.

7.4. Отличие в постановке и процессе решения вариационной задачи с закрепленными и свободными концами траектории движения объекта.

                                      Литература

1. Дегтярев Ю.И. Методы оптимизации: Учеб. пособие для вузов.-М.: Сов. радио, 1980.

2. Растригин Л.А. Современные принципы управления сложными объектами. - М.: Сов. радио, 1980.

3.Корщунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов М.: Энергоатомиздат, 1987.

Лабораторная работа  5

РАЗРАБОТКА И ИССЛЕДОВАНИЕ АЛГОРИТМА  ЛОГИЧЕСКОГО УПРАВЛЕНИЯ ТРАНСПОРТНОЙ СИСТЕМОЙ