Условия а) и г) связывают порядковые номера, которые получают работы, проводимые в оптимальной последовательности, поэтому формализация этих условий априори ничего не дает.
|
|
Система уравнений (10.5) может быть представлена в виде
|
|
или (после попарного вычитания строк)
Заметим, что всегда можно положить Δt0k(k=1,M), равными нулю (или, что то же, включить их условно в τ1k). Кроме того, работы подготовительные, регламентные и т. п. могут быть учтены наравне со всеми другими работами в общих соотношениях вида (10.5) — (10.7).
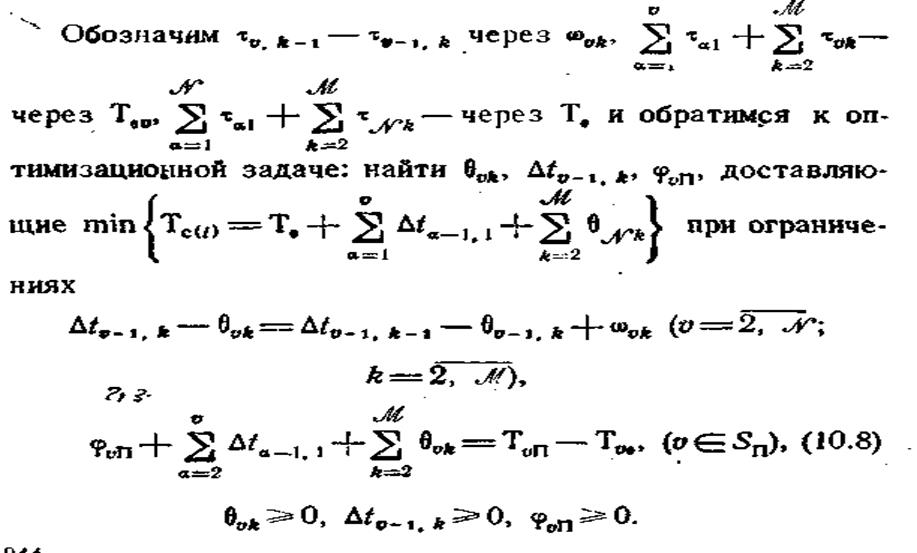
Зафиксировав произвольным образом все τvk, рассмотрим эту задачу как обычную задачу линейного программирования. Из выражения Tc(l) следует, что всякое допустимое базисное решение системы (10.8), содержащее в числе свободных переменные Δtv-1,1(v=2,N),ΘNk (k=2, M) будет оптимальным для сформулированной задачи. Однако подобные решения могут встретиться далеко не всегда, поэтому необходимы дополнительные исследования.
Обратимся к теореме (22): оптимальным является такое допустимое базисное решение (10.8), которое содержит в числе свободных все Δtv-1,1 и одновременно удовлетворяет требованиям ΘvkΔtv-1,k=0, (v=2,N, k=2,M) (переменная Θvk может войти в базис только тогда, когда Δtv-1,k является свободной и наоборот).
Доказательство этой теоремы основано на последовательном отделении заведомо свободных переменных Θvk (см. § 9.1). Чтобы найти оптимальные решения в каждом конкретном случае, достаточно использовать простое правило: если в очередной строке (10.8) сумма Δtv-1,k-1 — Θv-1,k + ωvkнеотрицательна, то в базис вводится Δtv-1,k , а Θvk считается свободной (равной нулю). Если же Δtv-1,k-1 — Θv-1,k + ωvk<0, базисной переменной становится Θvk, а Δtv-1,k обращается в нуль. Сформированное решение должно удовлетворять требованиям
φvП ≥0 (vЄ SП), иначе оно окажется недопустимым.
В этих условиях можно говорить об оптимальной организации работ даже при фиксированном порядке их производства (не нарушающем ограничений а) — г)). Так, этапы работы, выполняемой первой, должны следовать друг за другом без задержек (Θ1k=0, k=2, M); этапы любой промежуточной работы идут, вообще говоря, со сдвигами во времени один относительно другого. Исключение составляет случай, когда все
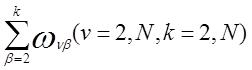неотрицательны.
Полученные результаты неконструктивны (они отвечают предположению τvk=const и не дают рекомендаций по выбору наилучшего плана проведения работ), однако появляется возможность отождествить произвольную перестановку столбцов матрицы ||τkv|| с некоторым показателем, вычисляемым довольно просто, что должно облегчить применение здесь метода динамического программирования (или методов, сходных с ним по идее). Условия для этого следующие:
— рассматривается N-шаговый процесс планирования;
— содержанием очередного шага является размещение того или иного столбца на определенной позиции;
— перед началом очередного шага возможны только Nсостояний процесса, причем параметр состояния скалярный (номер столбца).
Рассмотрим теперь время Tc(l) как функцию только τvk (v=1, N, k=1, M), имея в виду найденные решения. Оценка Ťc(i), получаемая при использовании рекомендаций приведенной выше теоремы и обозначаемая как Ťc(l), обладает рядом особенностей: в общем случае Ťc(l) представляет собой линейную комбинацию величин τvk, т. е.
|
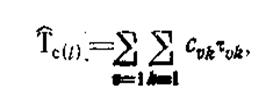
где cvk— целочисленные коэффициенты; каждое значение Ťc(l) отвечает заданному порядку работ, который в силу условия а) определяется порядком проведения их первого этапа (т. е. принятыми τv-1, (v=1,N), следовательно, τvkесть однозначно определенная функция
τv,1, (v=1,N).
Учитывая
эти замечания, получаем 
Ťc(l) =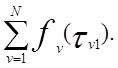 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
