Автоматизированные системы управления технологическими процессами: Методические указания к лабораторным работам и домашним заданиям, страница 14

Возможные наборы значений τ_v1 образуются при пере­становках N' элементов первой строки матрицы ║τ_kv║ , и множество всех таких перестановок объединяет N! эле­ментов. Наиболее удобным для практической реализации представляется метод поиска оптимума Ť_c(l)  по пере­менным τ_v1 основанный на идее непосредственного по­шагового формирования искомой расстановки работ и сводящийся к анализу промежуточных состоянии и наи­лучших продолжений процесса планирования. Исходны­ми данными здесь являются конкретизированные ограничения в), г) и матрица ║τ_kv║ с фиксированной произ­вольным образом нумерацией столбцов (исходная нумерация работ).

Основные этапы решения задачи: вводится предполо­жение о том, что (N— 1)-ю позицию занимает первая (по исходной нумерации) работа, и в рамках этого пред­положения исследуются варианты формирования двух последних позиций будущего плана («первая и вторая работы», «первая и третья работы», . . ., «первая и N-я работы»); для каждого такого варианта определяются ω_vk=τ_v,k-1- τ_v-1,k , Δt_v-1,k при v=N, k=2,M. Прове­ряется выполнение условий в), г) и оцениваются величины Ť_c(l)=Т_о + 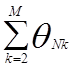. При проверках в) используются приближенные оптимистические показатели, вычис­ляемые для идеализированного случая, когда все Θ_vk , Δt_v-1,k (v=2,N-1; k=2,M) положены равными нулю. По мере накопления информации достоверность этих показателей растет, и в конечном счете они переходят в Ť_c(l). Вводится предположение о том, что (N— 1)-ю пози­цию занимает вторая (по исходной нумерации) работа, и в рамках этого предположения исследуются варианты формирования двух последних позиций плана («вторая и первая работы», «вторая и третья работы», . . ., «вто­рая и N-я работы»). Для каждого варианта отыскива­ются Θ_vk , Δt_v-1,k (v=2,N-1; k=2,M), проверяются усло­вия в), г) и оценивается Ť_c(l).

Рассмотренные операции повторяются для оставших­ся предположений, связанных с размещением третьей, четвертой, . . ., N-й работы на (N— 1) -й позиции. Таким образом, оказываются исследованными N(N— 1) ва­риантов, и становится возможным их сравнение с целью указать наилучшие из полученных Ť_c(l). (все это удобно свести в первую таблицу результатов, содержащую пе­речни вариантов, допустимых по ограничениям а) — г) и упорядоченных по признаку ухудшения Ť_c(l).).

Вводится предположение о том, что (N— 2) -ю пози­цию занимает первая (по исходной нумерации) работа. В рамках этого предположения исследуются варианты формирования трех последних позиций будущего плана, причем (N— 1) -я и N-я позиции (т. е. продолжение процесса) выбираются здесь как единое целое на основе использования данных первой таблицы результатов.

Определяются Θ_vk, Δt_v-1,k(v=2,N-1; k=2,M),проверяются условия в), г) (по оптимистическим показателям) и оцениваются новые величины

,М

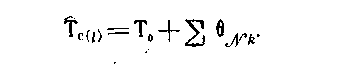
Все эти операции повторяются применительно к предпо­ложениям, связанным с размещением второй, треть­ей, . . ., N-й работ на (N— 2) -и позиции, так что общее число анализируемых вариантов составляет по-прежне­му N(N— 1). Все результаты, не нарушающие ограни­чений а) — г), сводятся во вторую таблицу.

Вводится предположение о том, что (N— 3)-ю пози­цию занимает первая (по исходной нумерации) работа, и исследуются варианты формирования четырех послед­них позиций будущего плана. Набор работ, попадающих па (N— 2)-ю, (N— 1)-ю, N-ю позиции, дает вторая таб­лица результатов; проводятся стандартные проверки условий в), г), вычисляются Ť_c(l)., и, наконец, составля­ется третья таблица результатов; переход к новым пред­положениям продолжается до тех пор, пока не будут со­ставлены и оценены последовательности из N работ.

Общее количество исследуемых вариантов в рассмо­тренной схеме не превысит N³ вместо N!при полном переборе (реальный выигрыш получается при N>5).