Работа состоит из двух частей. Первая часть представляет собой аналитическое исследование. Вторая часть заключается в численном моделировании полей на основе готовых компьютерных программ. Предполагается сопоставление полученных результатов.
Литература: П. Брито и др. Электростатические задачи в нелинейных средах. Статья в книге «Физика за рубежом 1988 Серия Б - преподавание». Сборник статей. М. Мир 1988. Стр. 24.
5. Задача о вращающемся неравномерно заряженном шаре
Шар радиуса R,
заряженный с объемной плотностью 
, где 
-
константа, вращается вокруг своей оси симметрии с постоянной угловой скоростью 
. Найти векторный потенциал А
и напряженность H магнитного поля внутри и снаружи шара. Построить
аналитическое и численное решения. Сравнить полученные результаты.
Литература: Джексон Дж. Классическая электродинамика. Гл. 5. М. Мир. 1965.
6. Задача о вращающемся неравномерно заряженном цилиндре
Бесконечный цилиндр радиуса R,
заряженный с объемной плотностью , где - константа, вращается вокруг своей оси с
постоянной угловой скоростью . Найти векторный
потенциал А и напряженность H магнитного поля внутри и
снаружи цилиндра. Построить аналитическое и численное решение. Сравнить
полученные результаты.
Литература: Джексон Дж. Классическая электродинамика. Гл. 5. М. Мир. 1965.
7. Задача о вращающейся неравномерно заряженной сфере
Сфера радиуса R,
заряженная по поверхности с плотностью 
, где - константа, вращается вокруг оси z с
постоянной угловой скоростью . Найти векторный потенциал
А и напряженность H магнитного поля в каждой точке пространства.
Построить аналитическое и численное решение. Сравнить полученные результаты.
Литература: Джексон Дж. Классическая электродинамика. Гл. 5. М. Мир. 1965.
8. Задача о токе, текущем по бесконечной эллиптической поверхности
По бесконечной эллиптической
поверхности с полуосями a и b параллельно ее оси течет ток с поверхностной
плотностью i = i1 при
0 < 
< 
и i = i2 при < < 2, где i1и i2
- постоянные векторы, - полярный угол, а ось z
совпадает с осью эллиптической поверхности и параллельна векторам i1и i2. Найти векторный потенциал А и напряженность H
магнитного поля в каждой точке пространства. Построить аналитическое и
численное решение. Сравнить полученные результаты. Исследовать случаи сонаправленных
и противоположно направленных токов.
Указание: для построения аналитического решения воспользоваться конформным отображением эллиптической поверхности на круговую, или ввести эллиптические координаты.
Литература: Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. Физматгиз, 1962.
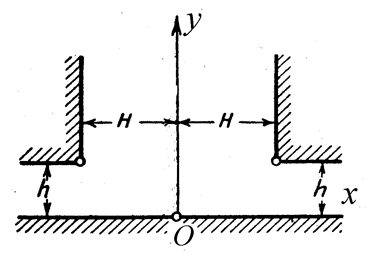
9. Задача о токовой нити над сложной поверхностью
Найти поле токовой нити с
током J, направленной перпендикулярно плоскости рисунка и находящейся
в области с магнитной проницаемостью 
в точке (x0, y0) (магнитная
проницаемость окружающего пространства 
).
Построить аналитическое и численное решения задачи. Сравнить полученные
результаты. Рассмотреть различные предельные случаи .
Указание: для построения аналитического решения воспользоваться конформным отображением Кристофера – Шварца.
10. Задача о токе, текущем по сложной цилиндрической поверхности
По бесконечной поверхности,
имеющей поперечное сечение в виде нормальной кривой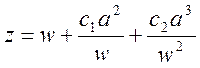 
,
параллельно ее оси течет ток с поверхностной плотностью i0 = const, ось z
совпадает с осью эллиптической поверхности и направлена в ту же сторону, что и
постоянный вектор i0.
Найти векторный потенциал А и напряженность H магнитного
поля в каждой точке пространства. Исследовать различные случаи 
и 
. Построить
аналитическое и численное решения. Сравнить полученные результаты.
Указание: для построения аналитического решения воспользоваться конформным отображением сложной цилиндрической поверхности на круговую.
Литература: Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. Физматгиз, 1962.
11. Магнитное экранирование
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.