Программа учебной дисциплины «Электродинамика» (Организационно-методический раздел. Содержание дисциплины. Учебно-методическое обеспечение курса), страница 15

30. Шар радиуса  a, являющийся абсолютно черным телом, находится в электромагнитном поле плоской линейно – поляризованной волны частоты . Длина волны мала по сравнению с радиусом . Определить результирующее поле дифрагированной волны и интенсивность dI рассеяния этой волны в телесном  угле  в среднем за период колебания волны. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

Методы изображений и инверсии в круге

1. Используя метод инверсии,  преобразуйте данную область (круговая лунка)  в диэлектрический клин с углом раствора  (центр инверсии М лежит на продолжении одной из сторон клина).

                          

М

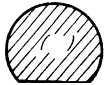
 2. Используя метод инверсии,  преобразуйте данную область (круговая лунка)  в диэлектрический клин с углом раствора  (центр инверсии М лежит на продолжении одной из сторон клина).

                           

            

      М

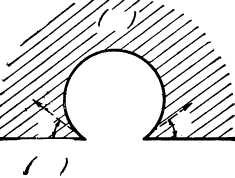
3. Используя метод инверсии,  преобразуйте данную область (круговая лунка)  в диэлектрический клин с углом раствора  (центр инверсии М лежит на одной из сторон угла).

                    

                 М 

           

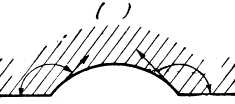
4. Используя метод инверсии,  преобразуйте данную область (круговая лунка)  в диэлектрический клин с углом раствора  (центр инверсии М лежит на одной из сторон угла).

                          

                          

      М

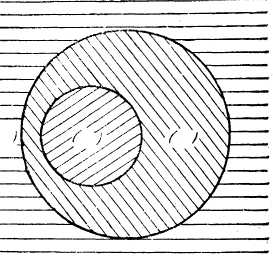
5. Используя метод инверсии,  преобразуйте данную область на концентрическое кольцо (центр инверсии М находится в первой среде с ).

      

                       

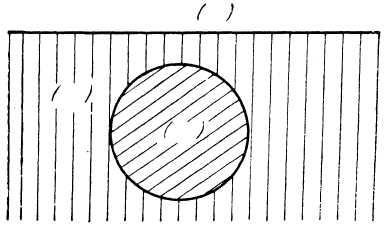
6. Используя метод инверсии,  преобразуйте данную область на концентрическое кольцо (центр инверсии М находится в первой среде с  ).

                                 

       

                           

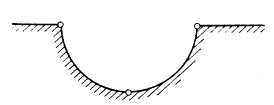
7. Используя метод инверсии,  преобразуйте данную область (круговая лунка) в диэлектрический клин с углом раствора  (центр инверсии М лежит на одной из сторон угла).

                         

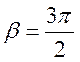
                                  М     

      

Метод конформных отображений

1. Найти поле токовой нити с током J, направленной перпендикулярно плоскости рисунка и находящейся  в области с магнитной проницаемостью  в точке (x₀, y₀) (магнитная проницаемость окружающего пространства ). Построить аналитическое и численное решения задачи. Сравнить полученные результаты. Рассмотреть различные предельные случаи .

                        

0                             a

2. Найти поле токовой нити с током J, направленной перпендикулярно плоскости рисунка и находящейся  в области с магнитной проницаемостью  в точке (x₀, y₀) (магнитная проницаемость окружающего пространства ). Построить аналитическое и численное решения задачи. Сравнить полученные результаты. Рассмотреть различные предельные случаи .

                           

            

        0            a

3. Найти поле токовой нити с током J, направленной перпендикулярно плоскости рисунка и находящейся  в области с магнитной проницаемостью  в точке (x₀, y₀) (магнитная проницаемость окружающего пространства ). Построить аналитическое и численное решения задачи. Сравнить полученные результаты. Рассмотреть различные предельные случаи .

                  

            0   a    

          

4. Найти поле токовой нити с током J, направленной перпендикулярно плоскости рисунка и находящейся  в области с магнитной проницаемостью  в точке (x₀, y₀) (магнитная проницаемость окружающего пространства ). Построить аналитическое и численное решения задачи. Сравнить полученные результаты. Рассмотреть различные предельные случаи .

                          

                          

0       a

5. Найти поле токовой нити с током J, направленной перпендикулярно плоскости рисунка и находящейся  в области с магнитной проницаемостью  в точке (x₀, y₀) (магнитная проницаемость окружающего пространства ). Построить аналитическое и численное решения задачи. Сравнить полученные результаты. Рассмотреть различные предельные случаи .