Программа учебной дисциплины «Электродинамика» (Организационно-методический раздел. Содержание дисциплины. Учебно-методическое обеспечение курса), страница 13

10. Электромагнитная волна, напряженность электрического поля которой , падает в нормальном направлении на плоский экран, имеющий бесконечную щель ширины 2a. Вектор поляризации  параллелен щели. Считая отклонение от геометрической оптики малым , определить электрическое поле дифрагированной волны, распространяющейся под малыми углами дифракции. Найти приходящуюся на единицу длины интенсивность dI рассеяния этой волны в интервале углов  в среднем по времени за период . Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

11. В плоском экране прорезаны N одинаковых бесконечных щелей ширины 2a. Расстояние между осевыми линиями соседних щелей 2b. Н экран в нормальном направлении падает плоская электромагнитная волна . Вектор поляризации  параллелен щелям. Длина волны мала по сравнению с характерными размерами  и , так что углы дифракции также малы. Определить электрическое поле дифрагированной волны и приходящуюся на единицу длины интенсивность dI рассеяния этой волны в интервале углов  в среднем по времени за период . Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

12. Плоский экран имеет прямоугольное отверстие со сторонами 2a и  2b. Монохроматическая плоская электромагнитная волна частоты  падает нормально к плоскости экрана. Вектор поляризации  параллелен одной из сторон прямоугольного отверстия, а длина волны мала по сравнению с характерными размерами  и . Определить электрическое поле дифрагированной волны и интенсивность dI рассеяния этой волны в телесном  угле  в среднем за период колебания волны. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

13. Ось полого кругового цилиндра радиуса а совпадает с осью z, а его торцы с плоскостями z = 0 и z = L. Потенциал  на  торцевой поверхности цилиндра z = L равен нулю, на поверхности z = 0 равен , а на боковой поверхности  - V(z) = 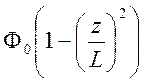. Найти потенциал в произвольной точке внутри цилиндра, если заряды в этой области отсутствуют. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

14. Найти поле токовой нити с током J, находящейся в точке (b, )  внутри бесконечной полой цилиндрической оболочки радиуса а, заполненной веществом с магнитной проницаемостью . Магнитная проницаемость окружающего пространства . Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

15. Определить магнитное поле линейного кругового тока J (радиуса b), находящегося внутри бесконечной полой цилиндрической оболочки радиуса а, заполненной веществом с магнитной проницаемостью . Магнитная проницаемость окружающего пространства . Центр витка совпадает с началом координат. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

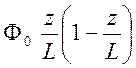16. Точечный заряд q находится внутри полого кругового цилиндра радиуса а в точке z₀ на оси симметрии цилиндра, которая совпадает с осью z. Торцы цилиндра совпадают с плоскостями z = 0 и z = L. Потенциал  на  торцевых поверхностях цилиндра равен нулю, а на боковой поверхности  - V = . Найти потенциал внутри цилиндра. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

17. Прямой круглый цилиндр длиной L и  радиуса а с однородной постоянной намагниченностью М, равной М₀, по величине и направленной вдоль оси z () помещен в немагнитную среду. Определить магнитное поле Н и магнитную индукцию В во всех точках, как внутри, так и вне цилиндра. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.

18. Точечный заряд q находится внутри полого кругового цилиндра радиуса а в точке z₀ на оси симметрии цилиндра, которая совпадает с осью z. Торцы цилиндра совпадают с плоскостями z = 0 и z = L. Потенциал  на  боковой и нижней поверхности цилиндра равен нулю, а на верхней поверхности  - V = . Найти потенциал внутри цилиндра. Построить аналитическое и численное решения задачи. Сравнить полученные результаты.