3.8. Перечень примерных задач, предлагаемых для решения на практических занятиях
Практические занятия по «Электродинамике» существенно опираются на использование навыков компьютерного моделирования, полученных при изучении курсов «Компьютерные средства и системы» и «Технологии компьютерного моделирования». Студентам предлагается решить одну и ту же задачу как аналитически, так и с использованием методов компьютерного моделирования в пакетах Ansys или Femlab, и провести анализ полученных решений. Основное внимание уделяется формированию умений оптимально выбирать и дифференцированно применять наиболее эффективные методы решения (как аналитические, так и численные), а также представлений о методах анализа полученного решения, оценке его эффективности и корректности.
Отчет по каждой задаче должен содержать:
- постановку задачи;
- решение задачи аналитически с указанием используемого метода;
- результаты компьютерного моделирования в пакетах Ansys или Femlab, текст программы;
- сравнение решений, полученных различными методами, их анализ и выводы об эффективности каждого из методов.
Ниже приводится примерный перечень задач по темам:
Основные понятия электромагнетизма
1.
Определить распределение объемной плотности j тока в
пространстве, если напряженность H
магнитного поля этого тока в пространстве имеет вид H = ![]() , где компоненты вектора H в сферических координатах
, где компоненты вектора H в сферических координатах 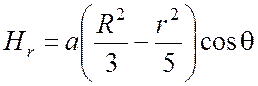 ,
, 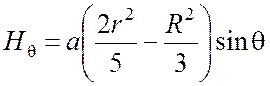 ,
, ![]() при
при ![]() ,
,
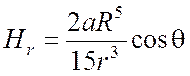 ,
, 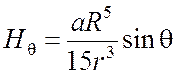 ,
, ![]() при
при ![]() .
Смоделировать полученное распределение объемной плотности тока, сравнить
результаты численного решения с заданным значением для поля.
.
Смоделировать полученное распределение объемной плотности тока, сравнить
результаты численного решения с заданным значением для поля.
2.
Определить распределение объемной плотности j тока в
пространстве, если напряженность H
магнитного поля этого тока в пространстве имеет вид H = ![]() , где компоненты вектора H в цилиндрических координатах
, где компоненты вектора H в цилиндрических координатах ![]() ,
, 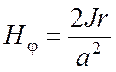 при r < a,
при r < a,
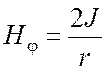 при
при ![]() ,
, ![]() при r > b.
Здесь a, b, J
– постоянные. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для поля.
при r > b.
Здесь a, b, J
– постоянные. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для поля.
3.
Определить распределение объемной плотности j тока в
пространстве, если напряженность H
магнитного поля этого тока в пространстве имеет вид H = ![]() , где компоненты вектора H в цилиндрических координатах
, где компоненты вектора H в цилиндрических координатах ![]() ,
, ![]() ,
, ![]() при
при ![]() ,
, ![]() ,
, 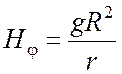 при
при ![]() . Здесь a,b,gи R
– постоянные. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для поля.
. Здесь a,b,gи R
– постоянные. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для поля.
4. В цилиндрических
координатах две компоненты векторного потенциала равны нулю ![]() , а третья имеет вид
, а третья имеет вид 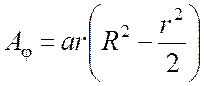 при r
при r![]() R,
R, 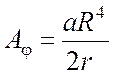 при r
при r![]() R,где a
и R – постоянные. Найти распределение объёмной плотности
j тока, создавшего магнитное поле с данным векторным
потенциалом. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для потенциала.
R,где a
и R – постоянные. Найти распределение объёмной плотности
j тока, создавшего магнитное поле с данным векторным
потенциалом. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для потенциала.
5. В сферических координатах
две компоненты векторного потенциала равны нулю ![]() , а
третья имеет вид
, а
третья имеет вид ![]() при r
при r![]() R,
R, 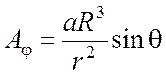 при r
при r![]() R, где a
и R – постоянные. Найти распределение объёмной плотности
j тока, создавшего магнитное поле с данным векторным
потенциалом. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для потенциала.
R, где a
и R – постоянные. Найти распределение объёмной плотности
j тока, создавшего магнитное поле с данным векторным
потенциалом. Смоделировать полученное распределение объемной плотности тока,
сравнить результаты численного решения с заданным значением для потенциала.
6. Объёмная плотность тока в пространстве меняется от точки к точке по периодическому закону j = j0 cos kr, где постоянные векторы j0 и k удовлетворяют соотношению kj0 = 0. Найти векторный потенциал A и напряжённость H магнитного поля, которые созданы этим током в неограниченном пространстве. Смоделировать полученное распределение объемной плотности тока, сравнить результаты численного и теоретического решений.
Метод разделения переменных в декартовой, цилиндрической и сферической системах координат
1. Полый параллелепипед
ограничен проводящими гранями, определяемыми шестью плоскостями x=0, y=0, z=0,
x=a, y=b, z=c. Найти потенциал ![]() в
произвольной точке внутри параллелепипеда, если на всех гранях параллелограмма
потенциал равен нулю, за исключением грани z=c, на
которой задано значение потенциала V(x,y)=cxy.
Внутри данной области заряды отсутствуют. Найти распределение поверхностной
плотности заряда на грани x=0. Построить аналитическое и численное решения
задачи. Сравнить полученные результаты.
в
произвольной точке внутри параллелепипеда, если на всех гранях параллелограмма
потенциал равен нулю, за исключением грани z=c, на
которой задано значение потенциала V(x,y)=cxy.
Внутри данной области заряды отсутствуют. Найти распределение поверхностной
плотности заряда на грани x=0. Построить аналитическое и численное решения
задачи. Сравнить полученные результаты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.