Компьютерное моделирование внешней зоны униполярного коронного разряда. Метод Дейча-Попкова. Коронный разряд в системе коаксиальных цилиндров

Компьютерное моделирование внешней зоны униполярного  коронного  разряда

Математическая модель внешней зоны униполярного корон­ного разряда. Основнуючасть пространства между электродами при униполярном коронном разряде занимает внешняя область, в которой движутся ионы только одного знака. Чехол коронного разряда, в котором сосредоточены ионизационные процессы, играет роль поставщика ионов для внешней зоны.

     Система уравнений для внешней зоны униполярного коронного разряда в установившемся режиме существенно упрощается и может быть представлена в виде:

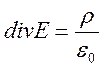    (1)

   (2)

         (3)

        

(4)

Граничными условиями для этой системы являются заданные значения потенциалов электродов и условие, которое гласит, что производная потенциала у поверхности коронирующего электрода равна начальной напряженности зажигания коронного разряда независимо от приложенного напряжения:

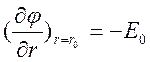            (5)

где r₀ – координата поверхности коронирующего электрода). Качественное объяснение этого, заключается в том, что при увеличении напряженности резко усиливаются ионизационные процессы в чехле коронного разряда, что приводит к возрастанию объемного заряда, выходящего за пределы чехла, а это в свою очередь ослабляет напряженность у электрода и уменьшает интенсивность ионизационных процессов. Имеются также экспериментальные подтверждения этого факта. Точные аналитические решения уравнений коронного разряда найдены только для систем электродов с простейшей геометрией (коаксиальные цилиндры и т.д.). Для сложных систем электродов, которые представляют практический интерес, найти точное аналитическое решение не представляется возможным, поэтому приходится искать дополнительные допущения, существенно упрощаю­щие задачу.

Метод Дейча – Попкова.

 Метод Дейча-Попкова базируется на дополнительном допущении о неиз­менности конфигурации силовых линий поля при коронном разряде по сравнению с элек­тростатическим полем. Это условие  приближенно выполняется даже при отсутствии ша­ровой или цилиндрической симметрии поля. Таким образом, полагая:

Eк = S E1       (6)

где S – некоторая функ­ция координат, можно рассчитать распределение напряженности и объемного заряда вдоль силовых линий поля.

Из уравнения Пуассона (1) с учетом (6) следует:

div S E₁=S div E₁+ E₁grad S=r/ee₀.       (7)

Из уравнений (3) и (4) аналогично следует:

div r bS E₁= r bS div E₁ + E₁grad rbS=0      (8)

Поскольку для электростатического поля div E₁ =0, то из (7) и (8) следует что:

E₁grad S=r/ee₀                             (9)

E₁grad rbS=0 (10)

Равенство нулю произведения векторов в (10) означает, что вектор gradrbS перпендикулярен Ё₁, т. е. произведение rbS постоянно вдоль силовой линии:

rbS=const = C₁                     (11)

Выявим еще одну особенность скалярной функции S. Из потенциального характера электрического поля следует что:

rotE_K = 0; rotE₁=0.    (12)

Тогда с учетом (6) согласно формулам векторного анализа получим:

rot E_k =S rot e_i + [grad S´E₁] = 0             (13)

  [grad S ´E₁] = 0         (14)

Из равенства нулю векторного произведения (14) следует, что вектор gradS направлен по силовой линии поля. Таким образом, функция S изменяется только вдоль силовых линий поля, т. е.

|grad S| = dS/dl         (15)

где l—расстояние вдоль силовой линии.

Записанные соотношения позволяют рассчитать распределе­ние напряженности вдоль силовых линий поля.

При подстанов­ке в - E₁ grad S=r/ee₀  - (9)

плотности объемного заряда r из (11)rbS=const = C₁

получим:

         S dS/dl         = C₁/b ee₀ E₁

и интегрировании от поверхности электрода с малым радиусом кривизны вдоль силовой линии получим:

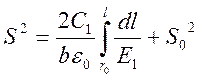  (16)

где S₀—значение функции S у поверхности электрода с малым радиусом кривизны.

Так как у поверхности коронирующего электрода:

E_k = S₀×E₁₂   =E₀             (17)

где E₁₂—значение электростатической напряженности у повер­хности электрода с малым радиусом кривизны,  то:

S₀  = E₀ / E₁₂        (18)

Кроме того,  умножая  обе  части  равенства  (11)  на  E₁ получаем

C₁=J/E₁ = J₀/E₁₂,        (19)

где  J₀—плотность  тока  коронного  разряда  на  поверхности электрода с малым радиусом кривизны. В результате получаем окончательное выражение для напряженности электрического поля:

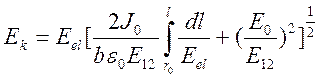      (20)

Для расчета напряженности поля при коронном разряде необходимо знать распределение напряженности электроста­тического поля E₁и значение плотности тока на поверхности коро­нирующего электрода J₀ или же в какой-то другой фик­сированной точке силовой линии в соответствии с (19). Эти значения плотности тока определяются из условия:

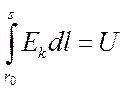   (21)

где s – координата поверхности не коронирующего электрода. Практически расчет ведется следующим образом:

1.  Производится расчет электростатического поля.

2.  Из уравнения вольтамперной характеристики или по экспериментальным данным для заданного напряжения U опре­деляется полный ток с коронирующего электрода I. По известной геометрии электрода находится ориентировочное значение J₀.

3.  Рассчитывается распределение напряженности поля E_kв соответствии с (20).

4.  Проверкой по (21) подтверждается принятое значение J₀. В случае необходимости расчет повторяется при уточненном значении J₀.

Данныйметод применим для расчета распределений напряженности электрического поля и плотности объемного заряда при коронном разряде в системах со сложной конфигурацией электродов.