Компьютерное моделирование внешней зоны униполярного коронного разряда. Метод Дейча-Попкова. Коронный разряд в системе коаксиальных цилиндров, страница 7

Моделирование униполярного коронного разряда в COMSOL Multiphysics.

В системе уравнений  в выражении для тока не учтена диффузия. Обычно при высоких напряжениях вклад миграционного члена намного выше диффузионного. В общем случае плотность тока с учетом диффузии следует записать в виде:  

С учетом диффузии система уравнений внешней зоны униполярного коронного разряда приобретает вид:

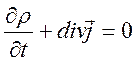                                                (2.1)

                                              (2.2)

                                            (2.3)

                                                       (2.4)

Объединяя выражения (2.3) и (2.4) и подставляя полученное  в (2.1), сведем систему к двум уравнениям с двумя неизвестными функциями ρ и φ:

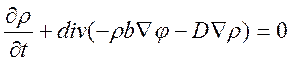                      (2.5)

                                              (2.6)

С появлением новых возможностей численного моделирования в Фемлаб становится реальным задать совместное решение двух уравнений с соответствующим набором начальных и граничных условий.

Предварительно следует переписать наши уравнения в терминах концентрации ионов, применив определение объемной плотности распределения электрических зарядов для случая униполярной проводимости: ρ=nze. С учетом этого систему 2.5-2.6 можно записать в виде:

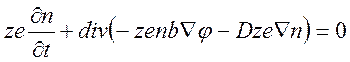
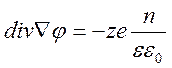
или

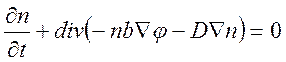                       (2.7)

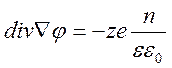                                          (2.8)

Для моделирования (2.7) воспользуемся уравнением Нернста-Планка без условия электронейтральности из раздела Application Modes – Chemical Engineering Module – Mass Balance – Nernst-Planck without Electroneutrality – Transient analysis (или, что то же самое, уравнение электрокинетического течения Electrokinetic Flow – Transient analysis). А для уравнения Пуассона (2.8) возьмем обобщенное дифференциальное уравнение в частных производных (Application Modes – COMSOL Multiphysics – PDE Modes – PDE, General Form):

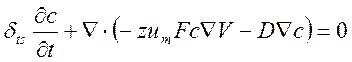            (2.9)

                                                         (2.10)

В обозначениях Фемлаб c – концентрация ионов, z – валентность, u_m – электролитическая подвижность, F – постоянная Фарадея, V – потенциал, D – коэффициент диффузии, δ_ts – коэффициент временного масштабирования; Г – в данном случае вектор напряженности электрического поля, F_s – функция источника.

По умолчанию все вычисления в Фемлабе производятся в системе СИ, поэтому необходимо установить соответствие между нашей системой измерения величин и системой СИ.

·  В исходных уравнениях концентрация - число ионов в единице объема задана в виде: 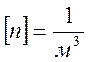количество ионов в объеме, в то время как в СИ размерность концентрации - 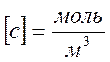. Между собой эти концентрации связаны числом Авогадро

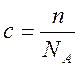
В молекулярно-кинетической теории количество вещества считается пропорциональным числу частиц. Единица количества вещества называется молем (моль). Моль – это количество вещества, содержащее столько же частиц (молекул), сколько содержится в 0.012 кг углерода ¹²C. Молекула углерода состоит из одного атома. Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной Авогадро N_A: N_A = 6.022∙10²³ моль^-1

Произведение числа Авогадро и модуля заряда электрона называется постоянной Фарадея , которая определяет соотношение между электрохимическими и физическими свойствами вещества. Постоянная Фарадея численно равна электрическому заряду, при прохождении которого через электролит на электроде выделяется 1/z моль z-валентность вещества. F = 96485.3415 Ас/моль

·  Коэффициенты диффузии имеют одинаковые размерности в обеих системах .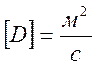

 Плотность тока в системе СИ можно записать в виде:

,

В терминах концентрации с и подвижности u токи можно записать так:

т.е.

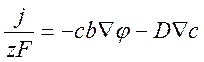
и

,