Коаксиальные цилиндры являются простейшей системой электродов, для которой уравнения (1)—(4) могут быть проинтегрированы непосредственно. В этой системе электродов метод Дейча – Попкова должен давать точные результаты, т.к. здесь, в силу симметрии задачи, силовые линии при коронном разряде не отличаются от электростатических. Принимая во внимание, что в цилиндрических координатах напряженность поля зависит только от текущего радиуса, можно записать для уравнения (1):
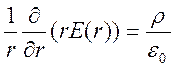 (25)
(25)
Обозначим через I ток короны на единицу длины электрода, тогда I= 2prJ0. Уравнение неразрывности (3) представим в виде:
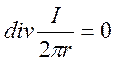 (26).
(26).
Уравнение (4), запишем в виде r=I/(2prbЕ). После подстановки последнего соотношения в (25) оно превратилось в уравнение, которое легко интегрируется:
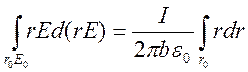 (27)
(27)
В результате получаем выражение для напряженности электрического поля:
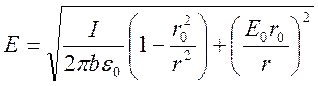 (28)
(28)
В этой формуле второй член в подкоренном выражении является маленькой поправкой. Он определяет поле в непосредственной близости от коронирующего электрода. Из решения системы (1-4) также может быть получено выражение для вольтамперной характеристики [1]:
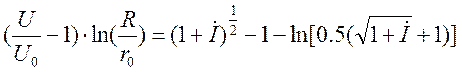 (29)
(29)
где: I = I/Iб,
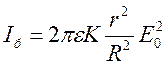
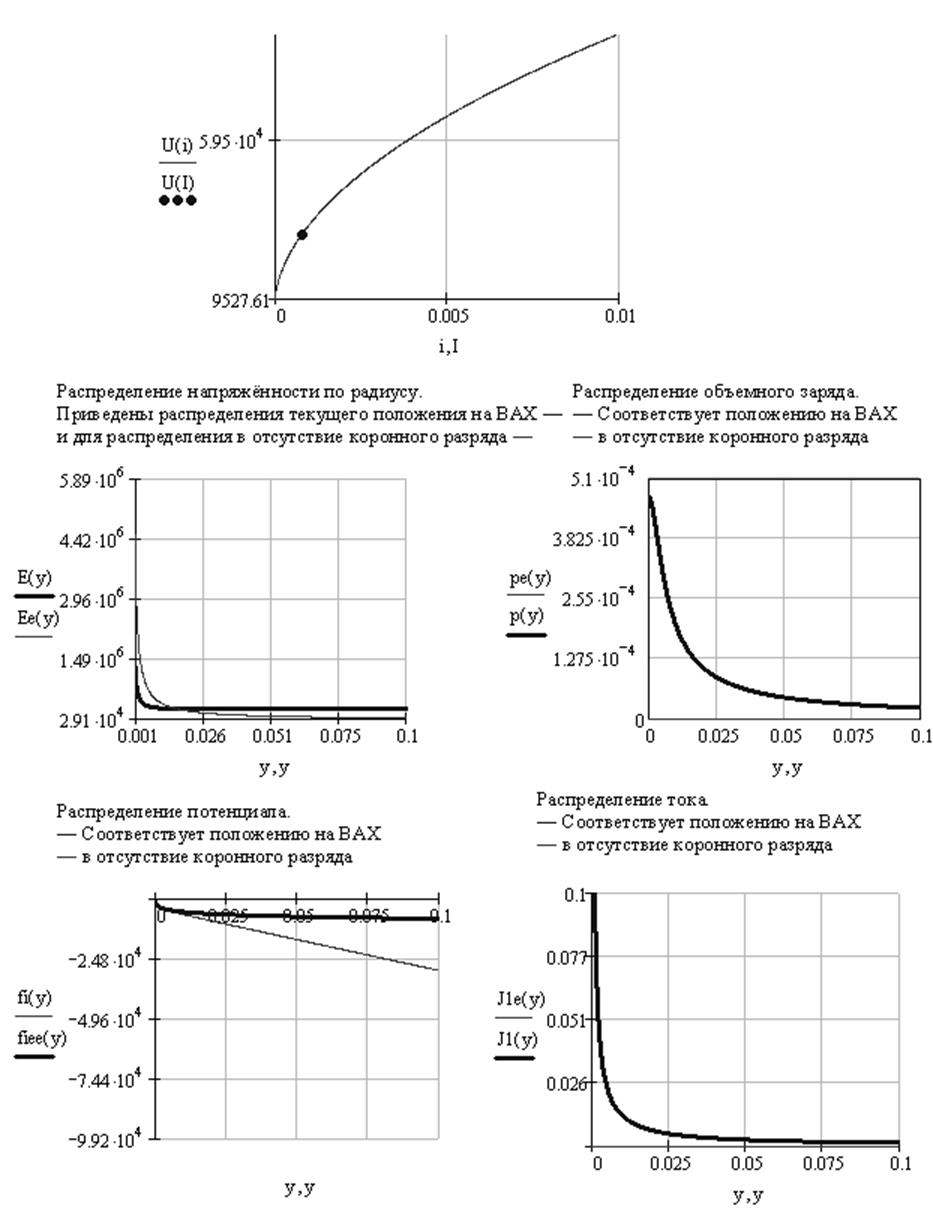
Ниже представлены результаты аналитического решения задачи об униполярном коронном разряде в системе коаксиальных цилиндров средствами MathCad:
Из формулы 2.20 следует, что при достаточно малом значении I задача становится линейной, что наглядно видно из приведенных ниже графиков.

Коронный разряд в системе электродов сфера – сфера.
В системе электродов, состоящей из двух концентрических сфер, уравнения коронного разряда так же могут быть решены аналитически. В такой геометрии электродов напряженность электрического поля зависит только от текущего радиуса. Уравнение (1) переписывается как:
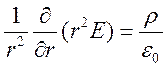 (32)
(32)
Пусть I полный ток с коронирующего электрода, тогда плотность тока выражается как:
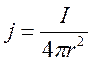 (33)
(33)
Выражая плотность объемного заряда из (4) и подставляя его в (32) с учетом (33) получаем уравнение:
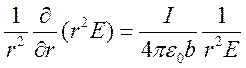 (34)
(34)
Решая уравнение (34) получаем выражение для напряженности электрического поля:
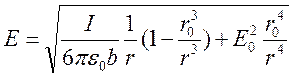 (35)
(35)
Плотность объемного заряда можно тогда выразить как:
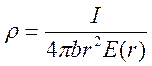 (36)
(36)
Эта система электродов интересна тем, что в отличие от всех систем, рассмотренных ранее, в ней все величины имеют более сильную расходимость. Как и в системе коаксиальных цилиндров метод Дейча – Попкова дает результаты, которые отличаются от аналитического решения менее чем на 1% как по напряженности электрического поля, так и по плотности объемного заряда. Это подтверждает применимость метода для моделирования коронного разряда.
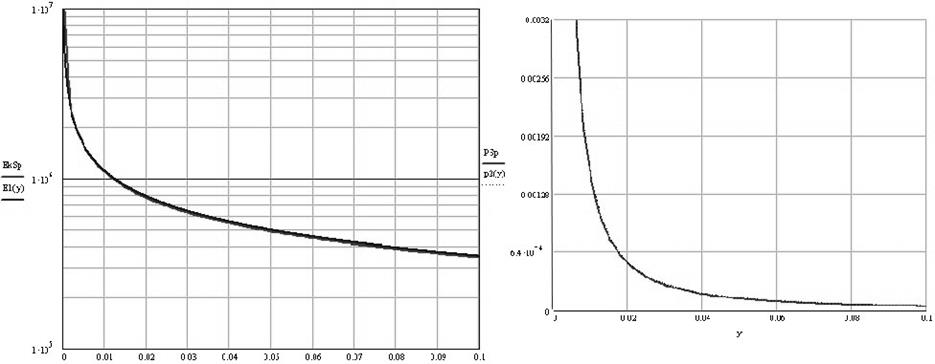
Рис. 17 Распределения напряженности электрического поля (слева) и плотности объемного заряда (справа) при коронном разряде между концентрическими сферами.
Красная линия – аналитическое решение.
Синяя линия – расчет методом Дейча – Попкова.
Было проведено сравнение распределений напряженности и потенциала электрического поля в системах цилиндр-цилиндр, провод – плоскость и концентрические сферы. Результаты представлены на рис. 18 - 19. Для системы провод плоскость была выбрана силовая линия выходящая под углом 00. Для всех систем U = 70 кВ, расстояние между электродами 10 см, радиус коронирующего электрода 2,5 мм.
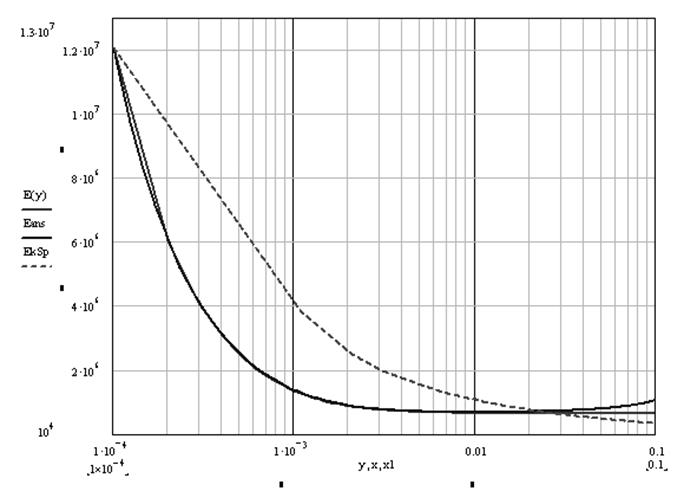
Рис. 18 Сравнение распределение напряженности электрического поля в различных системах электродов: Е(у) – коаксиальные цилиндры, Eans – провод над плоскостью, EkSp – концентрические сферы.
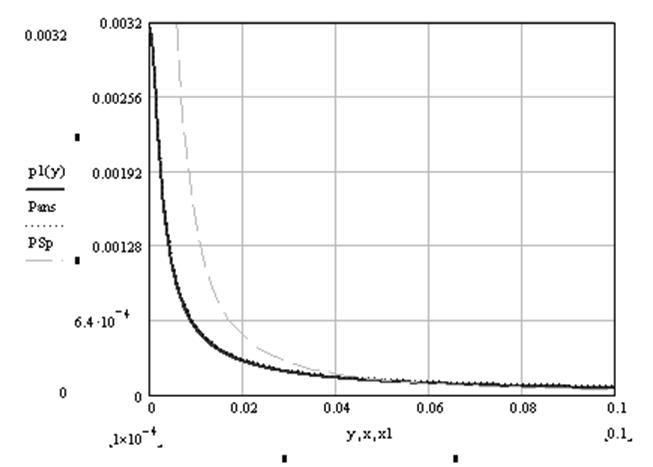
Рис. 19 Сравнение распределений плотности объемного заряда в различных системах электродов: p1(у) – коаксиальные цилиндры, Pans – провод над плоскостью, PSp – концентрические сферы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.