Компьютерное моделирование внешней зоны униполярного коронного разряда. Метод Дейча-Попкова. Коронный разряд в системе коаксиальных цилиндров, страница 2

Моделирование коронного разряда методом Дейча - Попкова в ANSYS

При моделировании, в качестве тестовой была выбрана система электродов провод над плоскостью. В соответствии с описанным выше алгоритмом моделирование коронного разряда в этой системе электродов проводилось в несколько этапов:

1.  Определение начальной напряженности зажигания короны Е₀ и плотности тока коронного разряда на поверхности электрода J₀.

2.  Расчет электростатического поля.

3.  Построение силовых линий электростатического поля.

4.  Расчет распределения электрического поля и объемного заряда вдоль силовых линий при коронном разряде.

5.  Уточнение значения J₀, расчет при уточненном значении J₀.

Для определения начальной напряженности зажигания короны использовалась эмпирическая формула Пика для цилиндрических электродов:

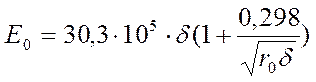     (22)

где d - относительная плотность воздуха, r₀ – радиус цилиндрического электрода (в сантиметрах). В эксперименте обычно определяется значение полного тока с коронирующего электрода. Пусть I полный ток на единицу длины электрода, тогда первоначальное значение (на первой итерации) J₀ определяется как:

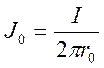      (23)

Весь дальнейший расчет проводился в пакете ANSYS. Для решения электростатической задачи использовался плоский элемент plane121. При расчетах радиус цилиндрического электрода варьировался от 0,1 мм до 2,5 мм. Расстояние от центра цилиндрического электрода до плского составляло 10 см. На цилиндрическом электроде задавалось значение потенциала 70кВ, на плоском 0 В. Результаты решения электростатической задачи для радиуса электрода 2,5 мм  представлены на рис.1.

Рис. 1  Распределение потенциала (слева) и напряженности электрического поля (справа) в электростатическом случае (напряжение 70 кВ, радиус электрода 2,5 мм).

Для того чтобы воспользоваться формулой (6), необходимо найти конфигурацию силовых линий электростатического поля. Построение силовых линий осуществлялось следующим образом: на поверхности коронирующего электрода задавалась начальная точка силовой линии, и задавалось приращение либо по x, либо по y координате (dx или dy соответственно). Таким образом, координаты следующей точки были (x+dx, y+dy), где dx и dy связаны соотношением: 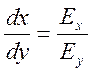. Найденная точка становилась исходной для нахождения следующей. При достижении противоэлектрода (или границы рассматриваемой области) процедура прекращалась. С помощью приведенного алгоритма было построено множество силовых линий, которые плотно заполняют всю рассматриваемую область (рис.2).

Рис. 2  Построенные в ANSYS силовые линии для системы провод над плоскостью.

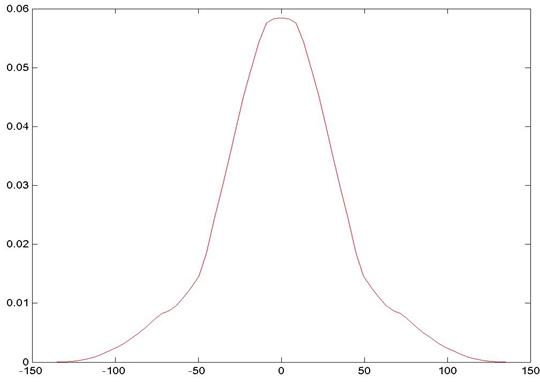
 Для каждой силовой линии, по распределению электростатического поля вдоль нее, вычислялось распределение напряженности поля при коронном разряде. При этом для каждой силовой линии подбиралось такое значение J₀, чтобы выполнялось соотношение (21). При этом учитывается неравномерность распределения плотности тока по поверхности коронирующего электрода. Полученное распределение плотности тока представлено на рис. 3. По горизонтальной оси отложен угол, который под которым выходит силовая линия электрического поля относительно линии, проходящей через центр цилиндрического электрода и перпендикулярной плоскому электроду. По оси ординат отложена плотность тока в А/м².

Рис. 3 Распределение плотности тока по поверхности электрода.

По формуле (20) было рассчитано распределение электрического поля вдоль каждой силовой линии. Распределение плотности объемного заряда рассчитывалось из:

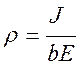                  (24).

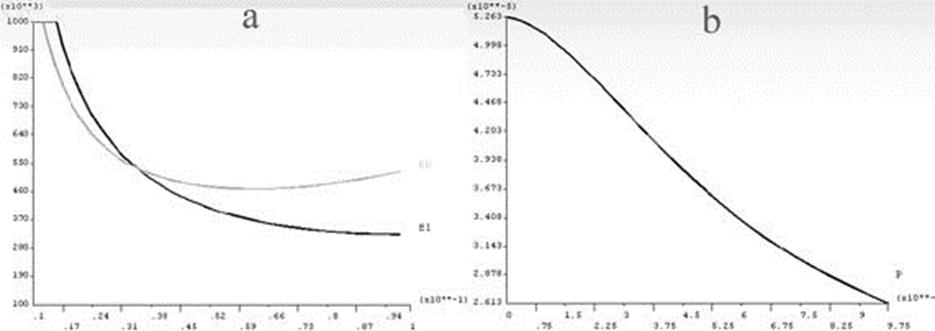
На рисунках ниже приведены распределения напряженности электрического поля в случае коронного разряда и без разряда, а также плотности объемного заряда вдоль различных силовых линий.