В пакете ANSYS уравнение Пуассона решается стандартным образом. Для решения уравнения неразрывности используется метод трубок тока. Этот метод можно рассматривать как способ численного интегрирования уравнения неразрывности (3), т.к. вдоль каждой из рассматриваемых трубок тока выполняется закон сохранения тока I=const, а, следовательно, и уравнение (3). Если в произвольной точке М на оси силовой трубки провести поперечное сечение, тогда плотность объемного заряда в точке М может быть определена как:
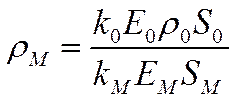 |
Наиболее существенные недостатки метода трубок: необходимость построения криволинейной сетки, связанной с силовыми линиями и изменяющейся от итерации к итерации, сложность и погрешность определения перпендикулярных сечений силовых трубок в общем случае.
В качестве тестовой задачи была выбрана система электродов провод-плоскость. Расстояние между электродами 10 см, приложенное напряжение 70 кВ, радиус коронирующего электрода 2 мм. Как уже говорилось выше, наибольшую сложность при данном методе решения системы уравнений представляет задание плотности объемного заряда на поверхности коронирующего электрода. В данной тестовой задаче в качестве известного было выбрано распределение, полученное при моделировании коронного разряда методом Дейча – Попкова. Было проведено 4 итерации. Ниже представлены результаты расчета:
На рис.1 представлены карты линий уровня отображающие изменение распределения плотности объемного заряда от итерации к итерации. Коронирующий электрод находится в начале координат. Плоский электрод находится внизу рисунка, на уровне 0.1. Значения плотности объемного заряда нормированы на максимальное значение для данной итерации.
Из рис.2 представлены распределения плотности объемного заряда (a) и напряженности электрического поля (b) вдоль линии проходящей через ось цилиндрического электрода и перпендикулярной плоскому (продольные профили). Из представленных рисунков видно, что действительно итерационный процесс быстро сходится. Так отличия между третьей и четвертыми итерациями не превышают 10%. Это так же видно на рис. 3 где представлены продольные профили (т.е. распределения вдоль линий параллельных плоскому электроду и лежащих в плоскости рисунка).
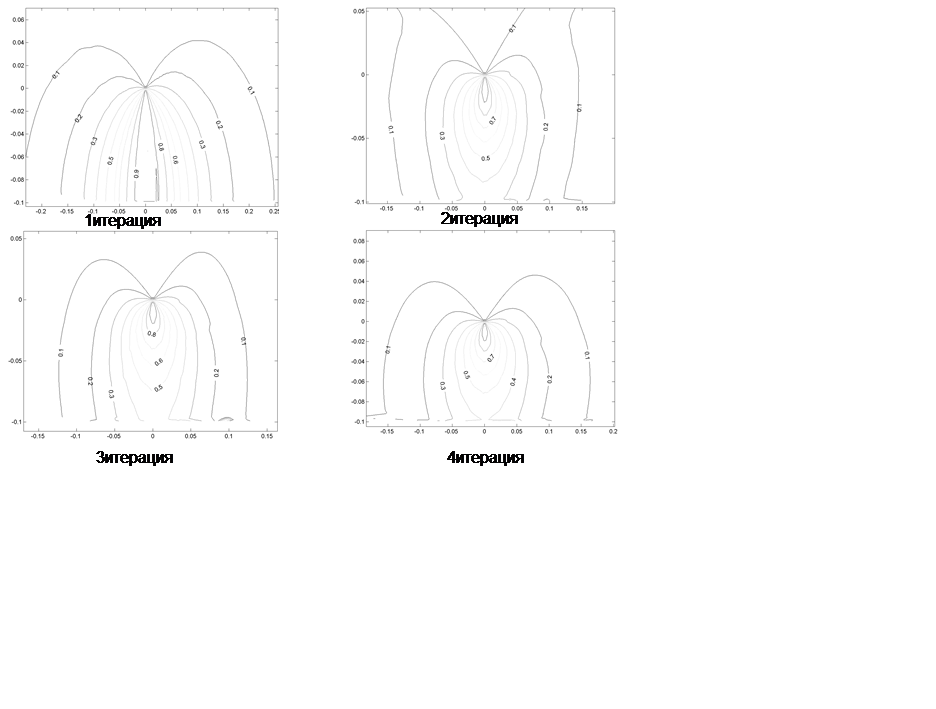
Рис.1 Изменение распределения плотности объемного заряда от итерации к итерации.
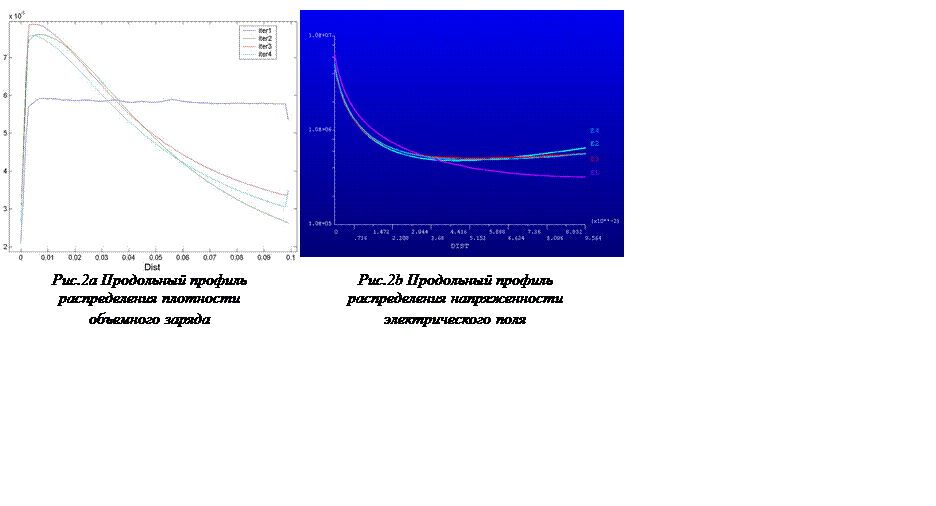
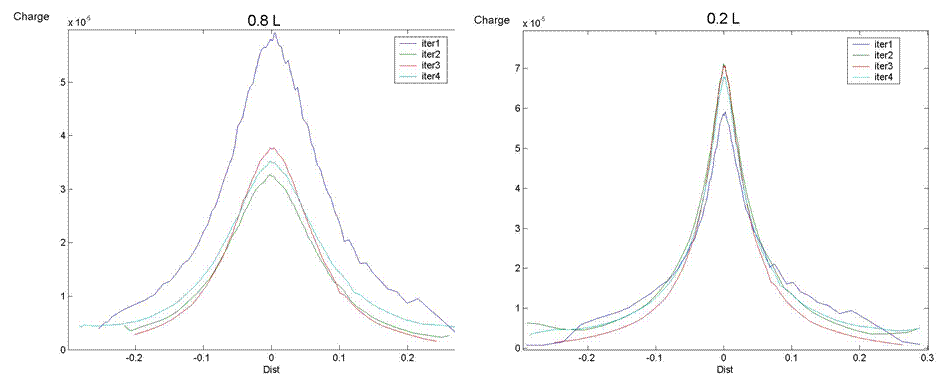
Рис.3 Распределение плотности объемного заряда (для различных итераций) вдоль поперечных профилей проведенных на расстоянии 8 см (слева) и 2 см (справа) от коронирующего электрода.
 Так как в данной
задаче распределение плотности объемного заряда около коронирующего электрода
было взято из результатов расчета методом Дейча-Попкова, то представляет
определенный интерес сравнить результаты численного решения системы уравнений с
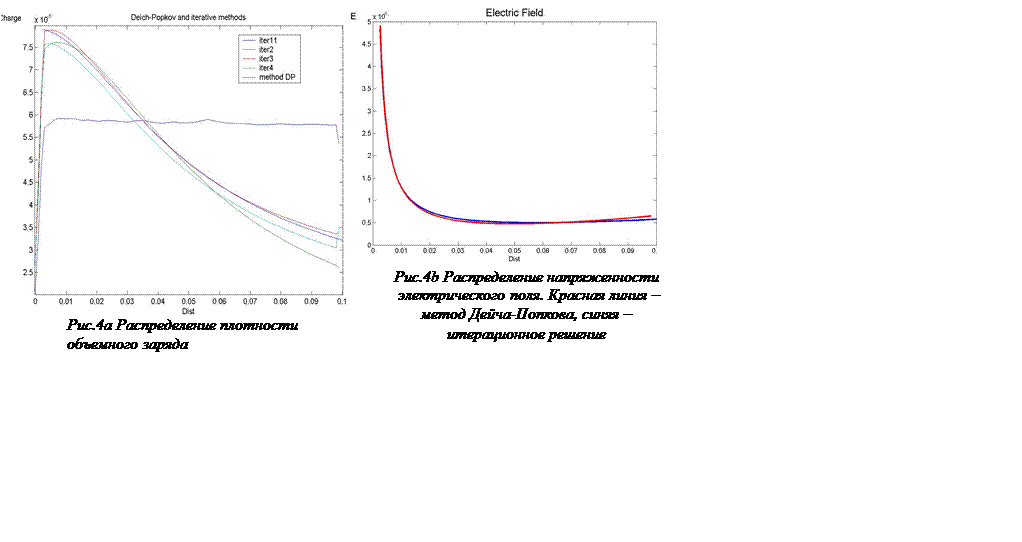
результатами моделирования методом Дейча – Попкова. На рисунке 4 представлены
распределения плотности объемного заряда (a) и
напряженности электрического поля (b) вдоль продольного
профиля. На рис.4a распределение посчитанное методом
Дейча – Попкова изображено синей линией, а распределение полученное итеративным
методом (4 итерации) красной линией. Как видно из этого рисунка плотность
объемного заряда и напряженность электрического поля для 4 итерации отличаются
незначительно (в пределах 5%).
Так как в данной
задаче распределение плотности объемного заряда около коронирующего электрода
было взято из результатов расчета методом Дейча-Попкова, то представляет
определенный интерес сравнить результаты численного решения системы уравнений с
результатами моделирования методом Дейча – Попкова. На рисунке 4 представлены
распределения плотности объемного заряда (a) и
напряженности электрического поля (b) вдоль продольного
профиля. На рис.4a распределение посчитанное методом
Дейча – Попкова изображено синей линией, а распределение полученное итеративным
методом (4 итерации) красной линией. Как видно из этого рисунка плотность
объемного заряда и напряженность электрического поля для 4 итерации отличаются
незначительно (в пределах 5%).
Таким образом, было проведено численное решение системы уравнений для внешней зоны униполярного коронного разряда в установившемся режиме в системе электродов провод – плоскость методом последовательных итераций. Итерационный процесс быстро сходится. Полученное решение согласуется с результатами моделирования униполярного коронного разряда методом Дейча – Попкова.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.