Компьютерное моделирование внешней зоны униполярного коронного разряда. Метод Дейча-Попкова. Коронный разряд в системе коаксиальных цилиндров, страница 5

Анализируя различные возможности численного решения уравнения неразрывности (3), можно выделить метод конеч­ных разностей, который наряду с направленным движением ионов позволяет учесть диффузионный перенос, и метод трубок тока. В последнем случае уравнение неразрывности записывается для каждой силовой трубки поля, на которые разбивается расчетная область. Из уравнения (3) находится изменение r вдоль каждой силовой трубки.                                                                            

Для того чтобы пояснить метод, основанный на уточнении решения Дейча — Попкова, запишем некоторые соотношения, следующие из системы уравнений (1) — (4).

Для выделенной силовой трубки сечением s и элементом длины dl уравнение (1) может быть записано в виде

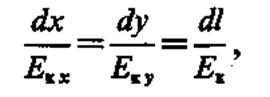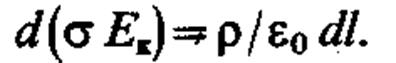Соответственно уравнение неразрывности (5.3) примет вид

где  J₀,  s_о — плотность   тока  и   сечение  силовой  трубки  на поверхности коронирующего электрода.

С учетом записанных соотношений интегрирование вдоль силовой трубки дает .

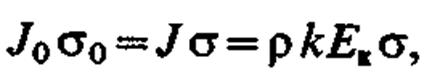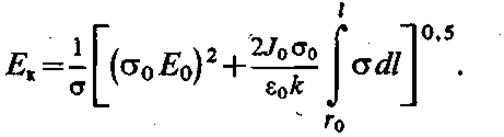Соотношение () используется для уточнения значений напряженности поля, если сечение силовой трубки определить по напряженности поля, рассчитанной на предыдущей итерации с учетом объемного заряда. При построении трубки тока используется уравнение силовых линий поля, которое определяет границы силовой трубки.

Метод трубок токов основан на получении решения методом итераций.

Трубки токов – объемы, ограниченные линиями тока. Вдоль трубки величина тока остается постоянной (условие неразрывности). Зная плотность объемного заряда вблизи электрода, можно вычислить объёмный заряд на протяжении всей трубки тока (зная площадь её сечения на каждом участке). Данный метод позволяет получать распределение объемного заряда по известной конфигурации поля, то есть осуществляет переход от уравнения (1) к уравнению (3). Полученное данным методом распределение  используется в качестве начальных данных при решении уравнения Пуассона на следующей итерации. Таким образом после решения задачи статики с начальным распределением  мы получим новое распределение силовых линий поля Е, а значит при очередном применении метода трубок токов получим и новое распределение объемного заряда. Повторяя эти действия несколько раз, получаем последовательные приближения решения. Задача начинает сходиться.

Между линиями тока определяется площадь сечения трубки тока (расстояние между линиями тока) и значение электрического поля. По полученным значениям вычисляется величина объемного заряда в этих точках и соответственно изменение проводимости в данной точке. Новое значение проводимости накладывается на элементы в качестве свойства материалов ANSYS. Снова решается задача токов с учетом объемного заряда.

      Таким образом при помощи данного метода нами производится решение уравнения неразрывности:

При этом по всей длине вычисляется значение объемного заряда для каждого конкретного участка трубки по следующей формуле:

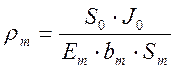
       - Подвижность электрона (в данной задаче - постоянная)

 - Величина электростатического поля

- Плотность  тока вблизи поверхности электрода. Определяется из  эксперимента (в данном случае берутся результаты из решения методом Дейча-Попкова)

- Площадь поперечного сечения трубки

Для численного решения системы уравнений (1) – (4) можно использовать схему организации итерационного процесса, на  каждой стадии которого из уравнения Пуассона (1) определяется распределение потенциала по заданной плотности объемного заряда, а полученные значения потенциала используются для уточнения распределения плотности объемного заряда путем решения уравнения неразрывности тока (3). Быстрая сходимость итерационного процесса обеспечивается тем, что на каждой итерации выполняются граничные условия. Однако граничные условия сложно реализовать по следующей причине: вместо заданного значения начальной напряженности Е_0, при организации последовательного решения уравнений, в явном виде участвует заданное распределение плотности объемного заряда у поверхности коронирующего электрода.