Компьютерное моделирование внешней зоны униполярного коронного разряда. Метод Дейча-Попкова. Коронный разряд в системе коаксиальных цилиндров, страница 8

Плотности тока j из уравнения Нернста-Планка в терминологии Фемлаба соответствует массовый поток частиц N.

Соотношения для подвижностей и токов таковы:

·  В последнем уравнении используется подвижность u. Она связана с подвижностью b соотношением

,

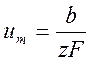причем размерность подвижности 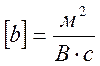, в Фемлабе используется т.н. электрохимическая подвижность, ее размерность – .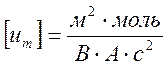

·  Соответствие плотности тока и массового потока ионов выглядит следующим образом:

,

,

.

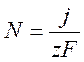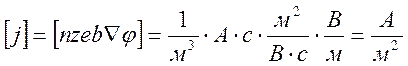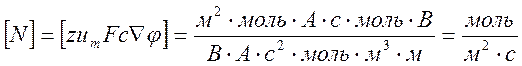Запишем уравнение Пуассона (2.8) в переменных концентрации c в следующем виде: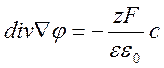  

В генеральной форме это уравнение следует переписать к виду: .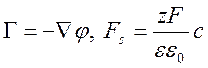

В соответствии с вышеизложенным конструируется система уравнений в Comsol:

δ_ts = 1 (коэффициент временного масштабирования)

D isotropic = D1 (коэффициент диффузии)

R = 0 (скорость реакции)

u_m = u1 (подвижность)

z = 1 (валентность)

u = 0 (скорость вдоль x)

v = 0 (скорость вдоль y)

V = phi (потенциал);

Г = (-phix, -phiy)

F = (zF/εε₀)с = (1*96485.3415)*с/(2*8.85∙10^-12) = 5.45∙10¹⁵с = 5.45e15*c

e_a = 0

d_a = 0

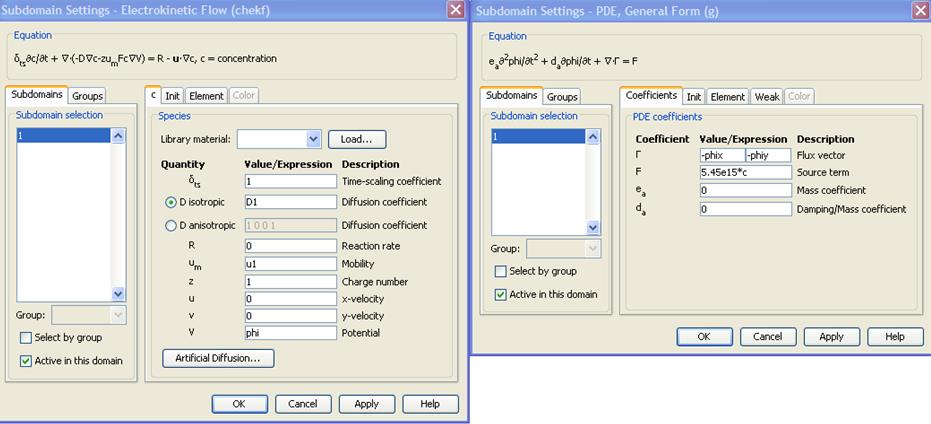
Концентрация c и потенциал phi являются искомыми функциями, и наличие V = phi в уравнении Нернста-Планка и Fs = Fs(c) в уравнении Пуассона обеспечивает их совместное решение.

Фемлаб позволяет задавать для уравнения Нернста-Планка граничные условия разного типа, а именно:

-  Граничное условие «поток» (Flux) констатирует, что поток частиц известен и задается функцией концентрации и потенциала

-  «Изоляция» выражается как

-  Можно установить значение концентрации с = с₀

-  В случае, когда весь массовый поток через границу обусловлен конвекцией, применимо условие «конвективный поток»

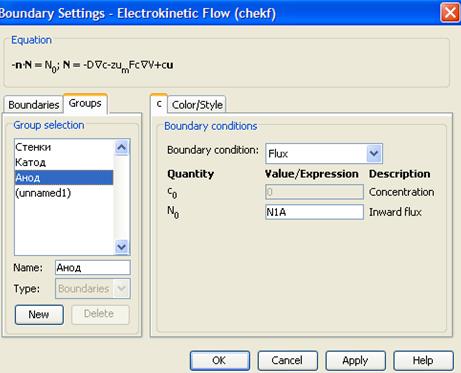
Будем рассматривать граничные условия в виде потоков ионов на электродах, проводя аналогию с коэффициентами рождения и гибели, используемыми в [8]. Будем называть их «токами рождения и гибели» соответственно.

Ток рождения задается константой N1A на аноде, а ток гибели задается на катоде пропорционально концентрации ионов: -N1K*c. Знак «минус» означает, что поток направлен «из объема».

  

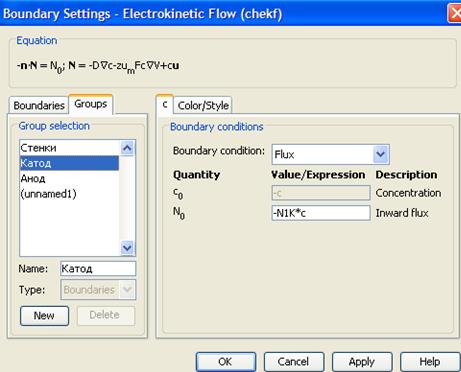
Для уравнения Пуассона возможны типовые граничные условия Дирихле и Неймана в виде значений искомых функций и их производных на границах рассматриваемых областей:

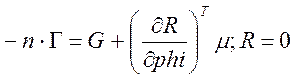 (условие Дирихле),

 (условие Неймана)

Воспользуемся условием Дирихле, чтобы задать разность потенциалов 1000 вольт на электродах: R = 1000-phi на аноде и R = 0-phi на катоде.

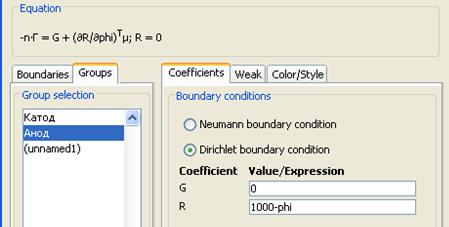
Рис. 2‑1. Окно ввода граничных условий.

В приложении к пособию приведены программы расчета и базы данных для нескольких значениях ионного тока на внутреннем электроде.

Результаты решения и их анализ.

Проанализируем решение для двух значений рожающегося на внутреннем электроде потока ионов равного N1A = 10^-17 и N1A = 10^-15.

На рис.  приведены последовательные во времени стадии распространения фронта концентрации ионов. Фронт концентрации движется от внутреннего электрода, на котором задано рождение. На рис. приведены распределения концентрации, напряженности поля и потенциала при различных рождениях.

Рассмотрим влияние тока рождения N1A при постоянном коэффициенте гибели на характер распределений концентрации, поля, объемного заряда и зависимость плотности тока от времени. В этой задаче объемный заряд вычисляется согласно формуле .

·  N1A = 10^-17.

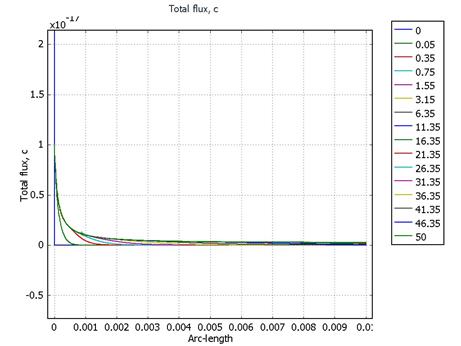
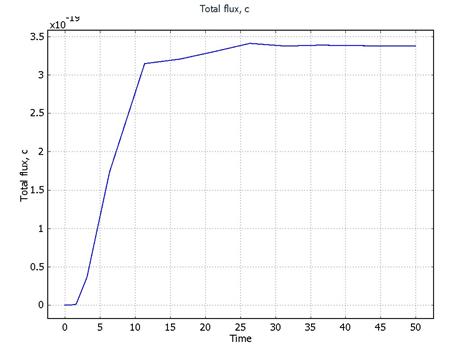
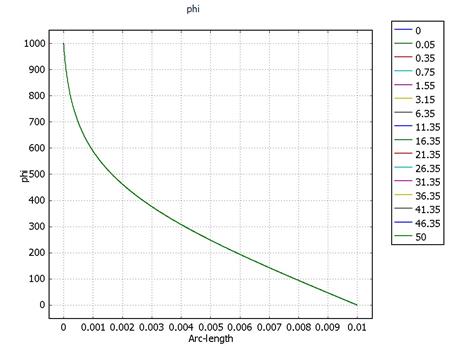
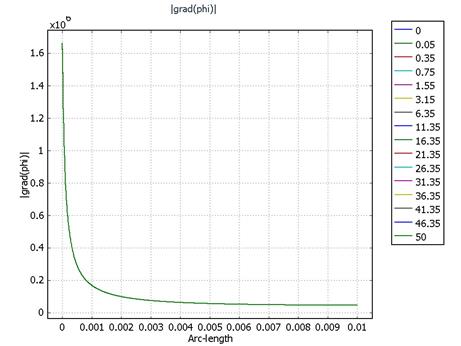
·  N1A = 10^-15.

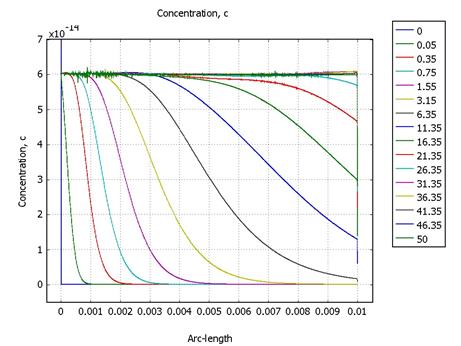
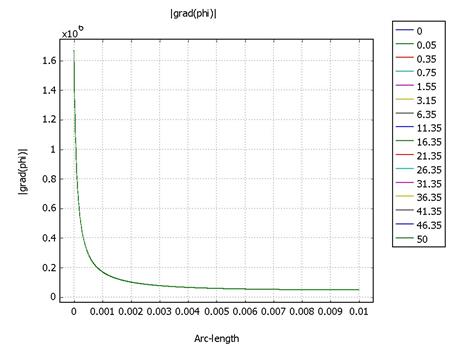
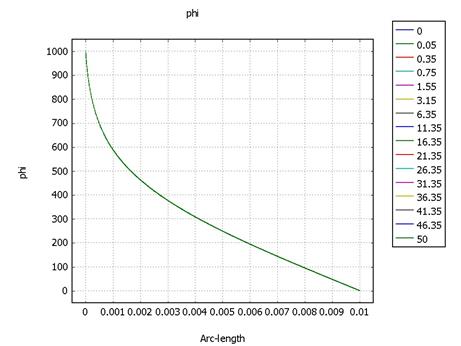
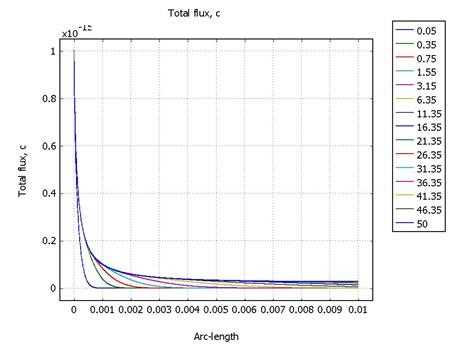
·  N1A = 1.5*10^-14

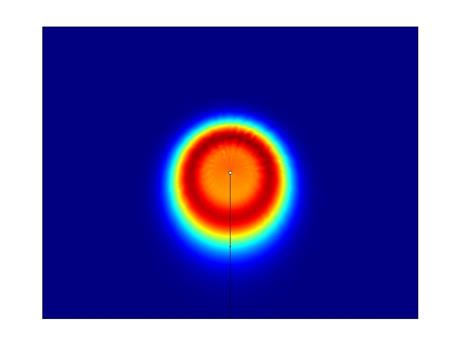
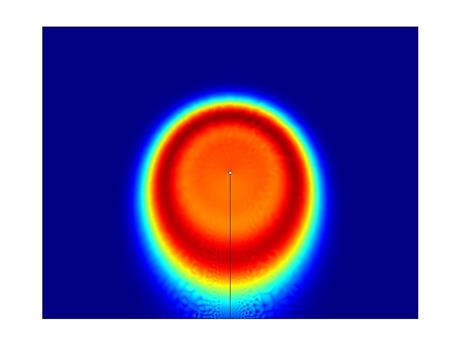
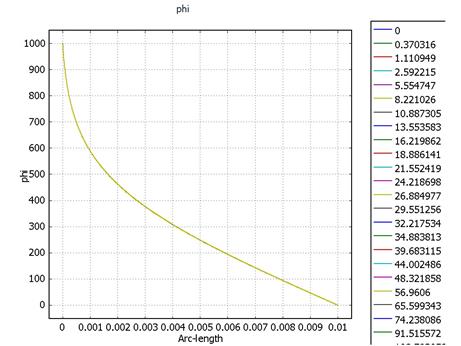
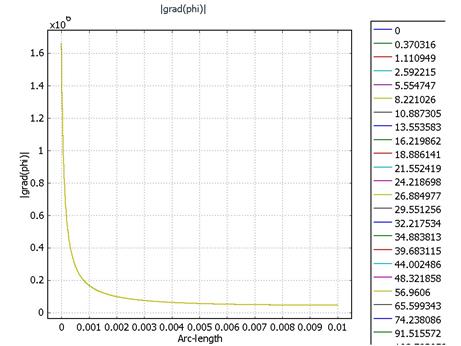
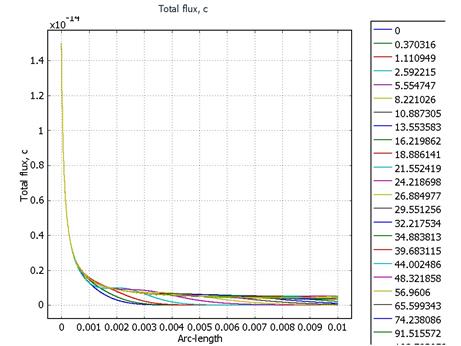
Распределения потенциала и напряженности неизменны во времени. От анода к катоду движется фронт концентрации и, достигнув стационара примерно через 40 секунд, распределяется в промежутке на уровне с = 6*10^-14. Это эквивалентно распространению объемного заряда за счет униполярной проводимости существует линейная связь с и ρ.