В данной лекции рассматривается решение задачи о коронном разряде в системе электродов нить-цилиндр. Кинетическое уравнение для электронов как и ранее решается в приближении Фоккера-Планка. Далее будет подробно рассмотрены обоснования возможности применения этого приближения.
Коронный разряд развивается в газах при давлениях порядка атмосферного в резко неоднородных электрических полях. Одна из систем с таким распределением поля – пара электродов нить-цилиндр (рисунок 1). Радиус внутреннего электрода должен быть много меньше радиуса внешнего. Такая установка имеется в высоковольтной лаборатории НИИ Радиофизики СПбГУ, именно возможностью сравнения результатов расчета с экспериментальными данными обусловлен выбор такой модели для численного решения.
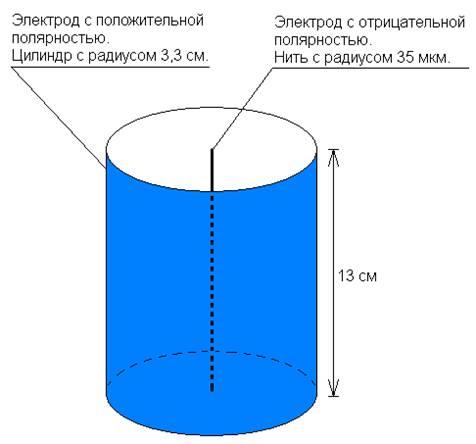
Рисунок 1. Конфигурация электродов «нить-цилиндр». Размеры соответствуют установке в высоковольтной лаборатории НИИ Радиофизики СПбГУ.
Однако при расчете коронного разряда в воздухе необходимо учитывать сложный химический состав, а также большое количество разнообразных реакций. В частности, большую роль здесь играет прилипание. Поэтому, учитывая новизну подхода, в начале рассмотрим расчетную модель для аргона - инертного газа, где нет прилипания и число существенных для хода процесса коронного разряда реакций минимально.
Простейшая система электродов – цилиндр-цилиндр. При достаточной высоте цилиндра можно пренебречь краевыми эффектами, и считать, что все величины в задаче зависят только от радиальной координаты r. Таким образом, задача становится одномерной. В CFD-ACE одномерных элементов нет, поэтому приходится строить формально двухмерную модель и ставить условия симметрии по аксиальной координате (рисунок 2). В конечноэлементной модели по аксиальной координате ставится минимальное число элементов (рисунок 3).
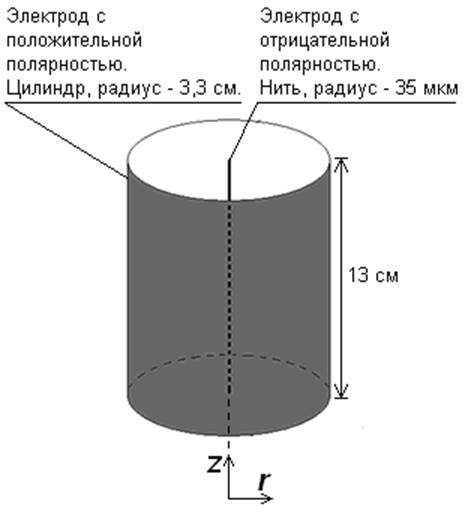
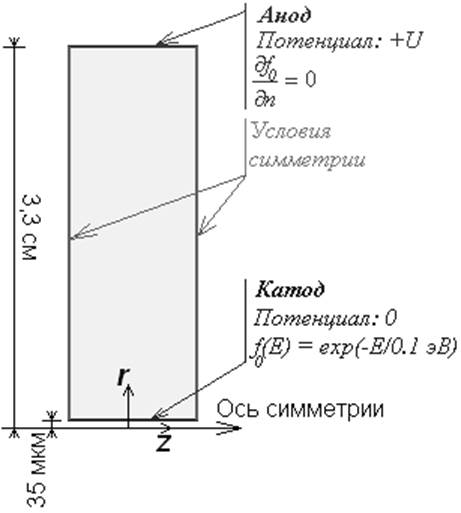
а) б)
Рисунок 2. а - конфигурация электродов «нить-цилиндр». Размеры соответствуют установке в высоковольтной лаборатории
НИИ Радиофизики СПбГУ.
б – модель в CFD-ACE с основными граничными условиями.
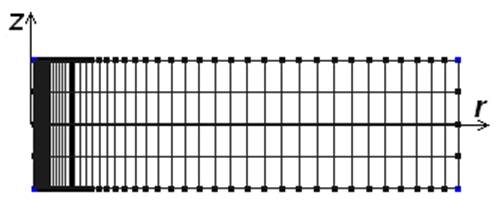
Рисунок 3. Конечноэлементная модель. Сетка сгущается к катоду – электроду с небольшим радиусом кривизны.
Для того, чтобы ионизация стала вероятной, необходимо одновременное соблюдение двух условий. Во-первых, электрон должен пройти достаточное расстояние – порядка длины пробега, даваемой формулой (1). Во-вторых, кинетическая энергия электрона должна превысить пороговую для данной реакции. Определим, какое условие в нашей задаче начинает выполняться раньше. Второе, таким образом, окажется условием запуска ионизации.
Сравним расстояние, на котором набирается энергия ионизации, и длину свободного пробега. Пусть потенциал равен нулю на внутреннем цилиндре и равен U на внешнем. Такая задача легко решается аналитически, потенциал зависит только от радиальной координаты r следующим образом:
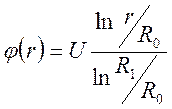 (1)
(1)
Зависимость логарифмическая. Электрическое поле направлено радиально, напряженность поля:
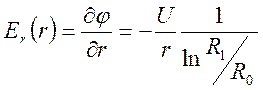
Стартовавший с катода электрон разгоняется полем, и, если пренебречь потерями на упругие столкновения, энергию электрона в эВ можно рассчитать по формуле (1), а его траектория будет соответствовать силовой линии поля (как только его энергия сильно превысит стартовую тепловую - 0,025 эВ). Конечно, так будет вплоть до первого неупругого столкновения.
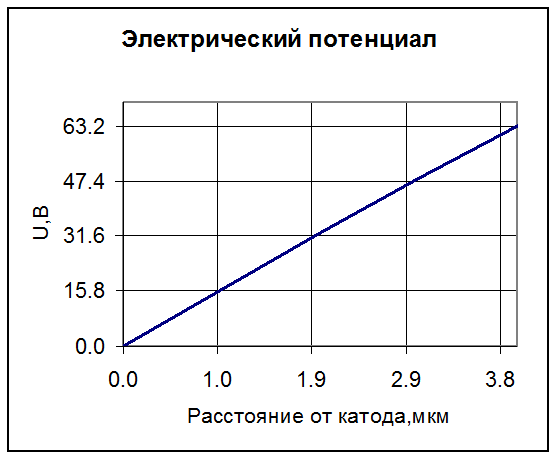
Рисунок 4. Электрический потенциал в окрестности катода.
На рисунке 4 приведена зависимость потенциала от радиальной координаты в окрестности проволочного электрода. По оси Y нанесены уровни, соответствующие одной, двум, трем порогам ионизации молекулы азота N2. На столь малом расстоянии от электрода зависимость практически линейная и размер зоны ионизации составляет 1,0 мкм.
Эта величина значительно меньше пробега по ионизации. Следовательно, нельзя считать, что ионизация с большой вероятностью произойдет, когда электрон наберет в поле кинетическую энергию, равную порогу ионизации. Ионизация произойдет позже, когда электрон накопит путь, равный пробегу по ионизации. Но рассчитать путь, пройденный электроном, достаточно сложно, поскольку, как показывалось выше, хаотическая составляющая скорости гораздо выше дрейфовой, и реальный путь, пройденный электроном, гораздо выше пути по дрейфу.
Итак, решение данной задачи требует анализа кинетического уравнения для электронов, которое учитывает распределение электронов по скоростям и является точным статистическим описанием ситуации. Единственным разумным приближением в данном случае может служить утверждение, что распределение электронов по направлениям скоростей почти равномерно. Это позволяет применить приближение Фоккера-Планка для кинетического уравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.