Компьютерное моделирование короны в различных газах, страница 3

В уравнении (5) используются данные других модулей – частота упругих столкновений ν рассчитывается исходя из функции распределения электронов по энергиям и концентраций тяжелых частиц, например, при учете столкновений лишь с частицами компонента №1:

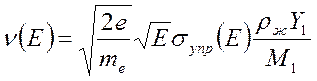                                                                   (6)

Также в уравнении (5) фигурирует электрический потенциал φ, рассчитываемый уравнением Пусассона (3).

Функция распределения f0 дает информацию о концентрации электронов:

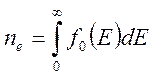                                                                                              (7)

Первая поправка на анизотропность распределения по скоростям позволяет вычислить плотность электронного тока.

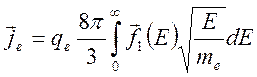                                                                             (8)

Как видно из системы (5), решение кинетического уравнения в приближении ФРЭЭ не требует задания подвижности электронов и коэффициента диффузии. Такие коэффициенты даже не фигурируют в уравнении, поскольку оно учитывает, что электроны c различной энергией имеют различные дрейфовые и тепловые скорости благодаря сильной зависимости сечений реакций от энергии электрона. Единственный фигурирующий в уравнении коэффициент χ, характеризующий диффузию электронов в фазовом пространстве координат и скоростей, вычисляется по данным о сечении реакции упругого столкновения. Частота столкновений дается формулой (6).

Но средняя дрейфовая скорость может быть подсчитана из решения как отношение потока электронов к электронной концентрации, которые даются формулами (7) и (8):

                                                                     

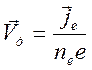
А подвижность вычисляется как отношение дрейфовой скорости к напряженности электрического поля:

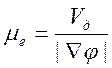                                                                                                      (9)

Таким образом, подвижность может существенно зависеть от координаты.

Надо сказать, что CFD-ACE, помимо основных неизвестных функций, которые непосредственно получаются при решении системы уравнений, выводит в файл решения большое количество производных величин. Это интенсивности реакций, потоки электронов и компонентов газа, коэффициенты диффузии и подвижности, плотность объемного заряда и многие  другие, поэтому самостоятельно вести вычисления по формулам (7)-(9) нет необходимости.

Вторичная эмиссия.

Необходимым условием самостоятельного установившегося коронного разряда является эмиссия электронов с катода. При не слишком больших напряженностях поля на поверхности металла (до 200 кВ/см) основным процессом рождения электронов является вторичная эмиссия, которая протекает по схеме:

                                                  

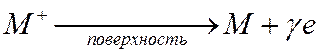
Здесь M⁺ - некоторый ион. На поверхности он нейтрализуется и может выбить из металла электрон. Коэффициент γ характеризует вероятность выбить электрон и называется коэффициентом вторичной эмиссии.

Вообще говоря, граничное условие вторичной эмиссии необходимо формулировать как условие на потоки частиц:

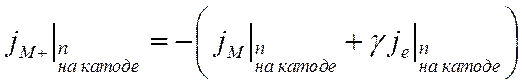                                                                                                              (10)

В CFD-ACE есть встроенная возможность задавать такое граничное условие, но, к сожалению, по неизвестной причине опция не работает. Проблема решается следующим образом.

Рассмотрим метод на примере газа аргона Ar. Вводится «виртуальная» частица Ar^- - атом аргона с электроном. Положительный ион выбивает из металла не электрон, а эту виртуальную частицу – для этого на катоде задается поверхностная реакция:

                                      

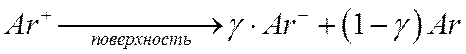
Далее необходимо быстро извлечь из «виртуальной» частицы Ar^- электрон. Для этого вводится объемная реакция с высоким коэффициентом скорости:

                                                       

Контролируется, чтобы все «виртуальные» частицы распадались на первом элементе вблизи катода. Можно проверить, что в результате у катода выполняется условие на потоки (10).