Теорія поля. Скалярне поле. Поверхні рівня. Градієнт. Векторне поле і векторні лінії. Потік вектора через поверхню

Лекція 11

Теорія поля

План:

 11.1. Скалярне поле. Поверхні рівня.

 11.2. Градієнт.

 11.3. Векторне поле і векторні лінії.

 11.4. Потік вектора через поверхню.

 11.5. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Щільність – плотность Втім –          вппрочем Окремий – отдельный Промінь – луч Приріст – приращение Вздовж – вдоль Спадання – убывание Прилеглі – прилежащие Кутова швидкість –           – угловая скорость

Можливе – возможное Найшвидше – быстрее                         всего Дотична – касательная Зтикалися – сталкивались Визначений –                – определённый Відповідний –             – соответствующий Передбачається –         – предусматривается

Спрямований – направленный Відбувається – происходит Обертання – вращения Випливає – вытекает Ділянка поверхні – участок                    поверхности Джерело – источник Порушується – нарушается Шуканий – искомый Відітнутої – отсечённой

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1.Нормований  вектор, або теж саме, що одиничний вектор колінеарний даному, або орт  вектора позначають так:  , координати цього вектора дорівнюють координатам вектора    поділеним на довжину ветора , тобто 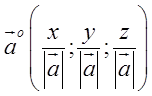, де – .

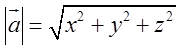2. Для того, щоб знайти проекцію вектора  на вісь  треба довжину вектора  помножити на косинкс кута між цим вектором і віссю  , тобто . З скалярного добутку одержимо, що 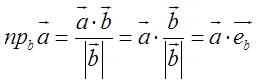, тобто проекція вектора   на вісь  рівна проекції цього вектора на напрямний вектор вісі , причому за напрямний можна взяти одиничний вектор .

3. Визначення похідної 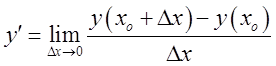 носить універсальний характер, основна вимога, щоб функція у при  була неперервною.

4. Рівняння нормалі в точці  до поверхні заданої  функцією  має вигляд 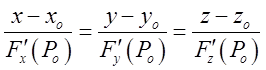. А якщо поверхня задана функцією , то рівняння поверхні має вигляд  .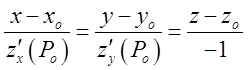

5. Геометричний смисл похідної  від функції  в точці  полягає в тому, що похідна  дорівнює , де  – кут, який утворює дотична до кривої  з додатнім напрямком вісі Ох.

6. Векторним добутком двох векторів називається такий третій вектор , який перпендикулярний двох попередніх, утворює з ними праву трійку і за довжиною дорівнює , де  – кут між векторами .

7. Для визначення вектора напруженості магнітного поля в точці , створюваного струмом, який тече по прямолінійному провідникові, застосовують закон Біо-Савара у векторно-диференціальній  формі 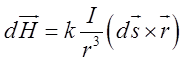, де  – вектор напруги магнітного поля, створеного струмом І, який проходить по дільниці  ;

  – вектор, проведений з початку вектора   в точку ,  в якій знаходимо напруженість. 

11.1.Скалярне поле. Поверхні рівня. Похідна за напрямком

Нехай в кожній точці Р деякої області  нам задане значення скалярної фізичної величини, тобто такої величини, що цілком характеризується своїм числовим значенням. Наприклад, це може бути температура точок нерівномірно нагрітого тіла, щільність розподілу електричних зарядів в ізольованому наелектризованому тілі, потенціал електричного поля і т.д. При цьому  називається скалярною функцією точки.

Область D, у якій визначена функція , може збігатися з усім простором, а може бути деякою його частиною.

Означення. Якщо в області D задана скалярна функція точки , то говорять, що в цій області задане скалярне поле.

Ми будемо вважати, що скалярне поле стаціонарне, т, е. що величина  не залежить від часу t. Зауважимо, втім, що в реальному оточені  приходиться зіштовхуватися і з нестаціонарними полями. Тоді величина  буде залежати не тільки від точки Р, але і від часу t.

Якщо фізична величина векторна, то їй буде відповідати векторне поле. Наприклад уже знайоме нам силове поле, поле швидкостей рухомого тіла, електричне поле напруженості, магнітне поле й ін. На практиці часто викликає інтерес скупчення точок, в яких значення скалярної функції приймає однакове значення. На площині множини таких точок утворюють лінії, в трьохвимірному просторі – поверхні. При складанні топографічних карт такі лінії означають однакову висоту місцевості над рівнем моря або глибину океану. На картах погоди – це може бути однакова температура, однаковий тиск, тощо. 

Означення.   Поверхнею рівня скалярного поля називається геометричне місце точок, у яких функція приймає постійне значення, тобто.

У курсі фізики при розгляді поля потенціалу поверхні рівня називають звичайно эквіпотенціальними поверхнями (тобто поверхнями рівного потенціалу).

Рівняння поверхні рівня, що проходить через дану точку  записується так: .                                                                           (11.1)

Якщо в окремому випадку скалярне поле плоске, тобто ми вивчаємо розподіл значень фізичної величини в якійсь плоскій області, то функція  залежить від двох змінних. Лініями рівня цього поля будуть лінії рівня функції . В геодезії, як зазначалось вище, це будуть лінії однакової висоти місцевості.

 Важливою характеристикою скалярного поля є швидкість зміни поля в заданому, напрямку.

Нехай задане скалярне поле, тобто задана функція . Візьмемо точку Р(х, у, z) і який-небудь промінь , що   виходить з неї. Напрямок цього променя задамо кутами ,  – це ті кути що цей промінь утворює  з напрямками осей Ох, Оу, Оz. (рис.11.1). Якщо  одиничний вектор, спрямований по промені , то його проекціями будуть направляючі косинуси: .