Теорія поля. Скалярне поле. Поверхні рівня. Градієнт. Векторне поле і векторні лінії. Потік вектора через поверхню, страница 5

Позначимо зміну віддаль між точкою О(0,0,0) і початком вектора  через t. Тоді  можна вважати як приріст t, тобто, якщо , то . Але ж  і тому . Очевидно, що , . Якщо  відстань від вісі Оz до точки , то .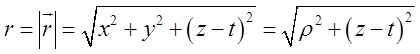

Розкриємо векторний добуток:

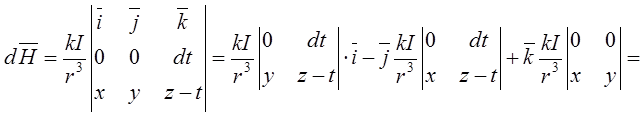
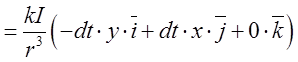. Бачимо, що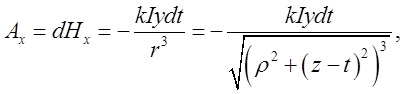

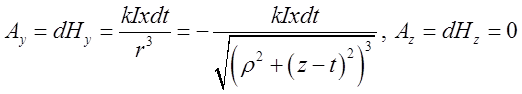. Щоб знайти  проінтегруємо знайдені диференціали в межах від  до .

=

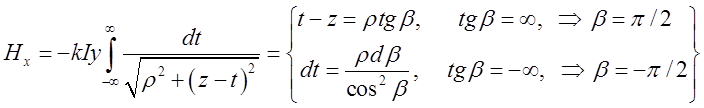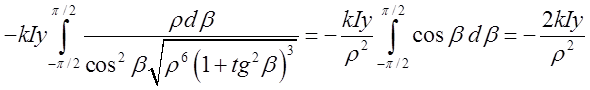=. Тобто 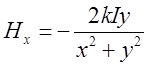. Аналогічно знайдемо 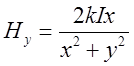. З .

Після скорочення знаменників на 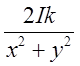,  диференціальні рівняння векторних ліній будуть мати вигляд: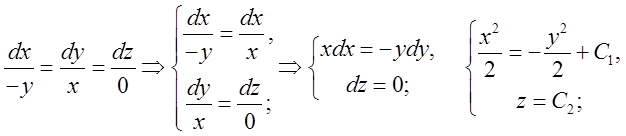   

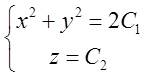 - це є рівняння сімейства кіл, центри яких знаходяться на вісі Oz; радіуси цих кіл  і віддалені вони від площини на віддаль.

11.4. Потік вектора через поверхню    

 Нехай векторне поле утворене вектором

Візьмемо в цьому полі деяку поверхню і виберемо на ній визначену сторону. Позначимо через  одиничний вектор нормалі до розглянутої сторони поверхні  у довільній її точці; проекціями вектора  служать направляючі, косинуси нормалі .

Розглянемо інтеграл по поверхні S від скалярного добутку вектора поля  на одиничний вектор  нормалі:

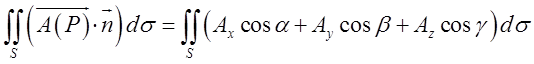
В попередній лекції  виражало поле швидкостей течії рідини і  тоді, як ми бачили, цей інтеграл  виражав потік рідини через поверхню S. У довільному  векторному полі цей інтеграл  будемо називати потоком вектора через поверхню S і позначати буквою К.              Oзначення. Потоком вектора через поверхню називається інтеграл по поверхні від скалярного добутку вектора поля на одиничний вектор нормалі до поверхні:

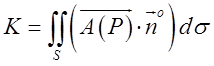                                                                                                           (11.7)

Таким чином, обчислення потоку вектора зводиться до обчислення інтегралу по поверхні. Із самого оначення випливає, що потік вектора К величина скалярна. Якщо змінити напрямок нормалі  на протилежний, т. е, змінити сторону поверхні інтегрування, то потік К змінить знак. Тому, що скалярний добуток вектора  на одиничний вектор нормалі  дорівнює – проекції вектора  на напрямок, то потік К можна представити у вигляді 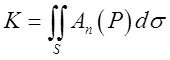. Зрозумідо, що .

Звідси, зокрема, випливає, що якщо на деякій ділянці поверхні проекція вектора  на нормаль постійна: , то потік через таку ділянку поверхні просто дорівнює  ,                                                                                         (11.7а)

 де Q – площа ділянки поверхні.                             1

Приклад.

Особливий інтерес представляє випадок, коли S – замкнута поверхня, що обмежує деяку область . Якщо береться зовнішня нормаль, то ми будемо говорити про потік зсередини поверхні S. Він позначається так:

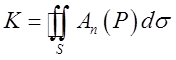                                                                                         (11.8)

Відзначимо також, що в курсах фізики і прикладних дисциплін інтеграли по поверхні (зокрема, подвійні) і навіть потрійні інтеграли дуже часто позначають за допомогою одного знакy интеграла. При такому способі запису інтеграли розрізняються за позначеннями диференціала і області інтегрування: 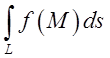 означає интеграл по лінії, 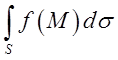  – інтеграл по поверхні, 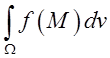 інтеграл по об’єму.

Коли векторне поле  представляє поле швидкостей рідини, величина потоку K дає різницю між кількістю рідини, що витікає з області  і кількістю рідини, що вливається в цю область. Якщо К=0 в область  рідини вливається стільки ж, скільки і витікає. Так, наприклад, буде для будь-якої області, розміщеній у потоці води, що тече в річці.

Якщо ж величина К відмінна від нуля, наприклад позитивна, то з області  рідини витікає більше, ніж вливається. Це означає, що в області  існують джерела, що збільшують потік рідини. Навпаки, якщо величина К від’ємна, то це вказує на наявність стоків – місць, де рідина видаляється з потоку.

П.7. Знайти потік векторного поля

через верхню сторону трикутника А В С  з  вершинами в точках А(1,0,0), В(0,1,0), С(0,0,1).

Розв. Рівняння площини, у якій лежить трикутник А В С, має вигляд , відкіля . Трикутник А В С проектується взаємно однозначно на площину хОу в область , яка обмежена трикутником ОАВ (мал. 18).

За умовою нормаль  до площини, у якій лежить трикутник АВС, утворить гострий кут у з віссю Оz, тому . Використовуючи градієнт, знайдемо одиничний вектор :    .

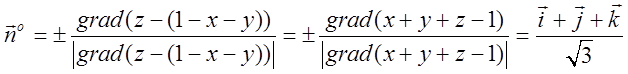
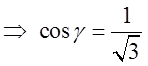Знаходимо скалярний добуток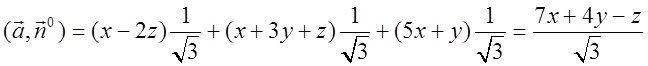

Застосовуючи формулу (11.7), обчислюємо шуканий потік:

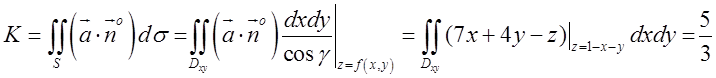 .Відп. 5/3.

П.8. Знайти потік векторного поля 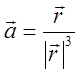через сферу радіуса R з центромнапочатку координат.