Нехай точка ![]() лежить на промені
лежить на промені ![]() ; відстань позначимо через
; відстань позначимо через ![]() .
Проекції вектора
.
Проекції вектора ![]() на вісі координат будуть рівні
на вісі координат будуть рівні ![]() , але з іншогобоку ці проекції є різниці координат: кінцевої і
початкової
, але з іншогобоку ці проекції є різниці координат: кінцевої і
початкової ![]() . Отже,
. Отже, ![]() .
А звідси
.
А звідси ![]() . Розглянемо приріст функції функції
. Розглянемо приріст функції функції ![]() при переході від точки
при переході від точки ![]() до точки
до точки ![]() :
:
![]() .
.
Зрозуміло, що коли точка ![]() буде
змінювати своє положення на промені
буде
змінювати своє положення на промені ![]() , то
в виразі для різниці
, то
в виразі для різниці ![]() буде
зміннюватися тільки величина
буде
зміннюватися тільки величина ![]() . Щоб визначити похідну
вздовж променя
. Щоб визначити похідну
вздовж променя ![]() треба знайти границю відношення
треба знайти границю відношення
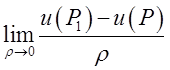 . А тому для похідної за напрямком маємо
таке
. А тому для похідної за напрямком маємо
таке
Означення.
Похідною від функції ![]() у
напрямку
у
напрямку ![]() в точціР називається границя (якщо вона існує)
в точціР називається границя (якщо вона існує) 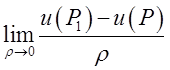 =
=
=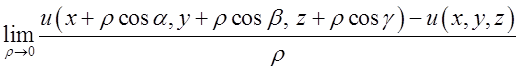 . (11.2)
. (11.2)
Цю границю будемо позначати символом ![]() чи
чи
![]() . Величина її залежить від обраної точки Р(х,у,z ) і від напрямку променя
. Величина її залежить від обраної точки Р(х,у,z ) і від напрямку променя ![]() , тобто від
, тобто від ![]() .
Якщо точка Р фіксована, то величина похідної буде залежати тільки від
напрямку променя. З визначення похідноїза напрямком випливає, що якщо напрямок
.
Якщо точка Р фіксована, то величина похідної буде залежати тільки від
напрямку променя. З визначення похідноїза напрямком випливає, що якщо напрямок ![]() збігається з додатним
напрямком осі Ох, тобто
збігається з додатним
напрямком осі Ох, тобто 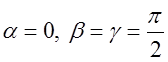 . Границя (11.2) буде просто дорівнювати частинній
похідній від функції
. Границя (11.2) буде просто дорівнювати частинній
похідній від функції ![]() по х:
по х: 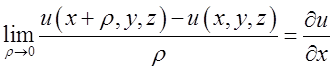
![]()
Аналогічну картину ми одержимо, якщо напрямок ![]() буде
збігатися з напрямками осей Оу й Оz.
буде
збігатися з напрямками осей Оу й Оz.
Подібно тому
як частинні похідні ![]() характеризують
швидкість зміни функції у напрямках осей координат, так
і похідна по напрямку
характеризують
швидкість зміни функції у напрямках осей координат, так
і похідна по напрямку ![]() буде швидкістю зміни функції
буде швидкістю зміни функції ![]() у точці Р по напрямку променя
у точці Р по напрямку променя
![]() .
.
Абсолютна
величина похідної ![]() у напрямку
у напрямку ![]() визначає
величину швидкості, а знак похідної характер зміни функції
визначає
величину швидкості, а знак похідної характер зміни функції ![]() ( зростання чи спадання).
( зростання чи спадання).
Для практичного обчислення похідної по напрямку користуються наступною теоремою.
Теорема.
Якщо функція ![]() диференційовна,
то її похідна
диференційовна,
то її похідна ![]() по будь-якому напрямку
по будь-якому напрямку ![]() існує і дорівнює
існує і дорівнює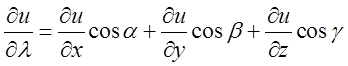 (11.3)
(11.3)
де ![]() напрямні
косинуси променя
напрямні
косинуси променя ![]() ,
або координати одиничного вектора напрямку променя
,
або координати одиничного вектора напрямку променя ![]() .
.
Доведення. Так, як функція ![]() диференційовна, то її повний приріст можна записати у вигляді:
диференційовна, то її повний приріст можна записати у вигляді: ![]()
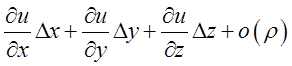 , де
, де ![]() . Як це добре видно з рис 11.1, (
. Як це добре видно з рис 11.1, (![]() –прилеглі катети)
–прилеглі катети) ![]() ,
а тому різницю
,
а тому різницю ![]() представимо
у вигляді
представимо
у вигляді 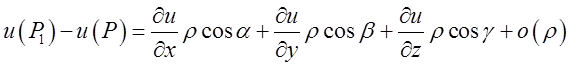 .
.
Знайдемо границю відношення 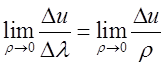 . Очевидно ця границя
дорівнює
. Очевидно ця границя
дорівнює 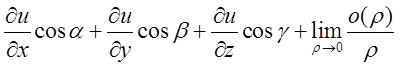 так, як значення частинних похідних
так, як значення частинних похідних 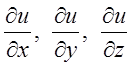 в точці Р, а
також
в точці Р, а
також ![]() від
від ![]() не
залежать, то, переходячи до границі при
не
залежать, то, переходячи до границі при ![]() одержимо
одержимо 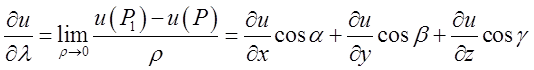
що і потрібно було довести.
11.2. Градієнт
Розглянемо знову формулу для похідної по напрямку 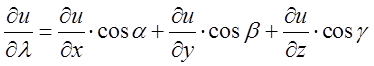 . Вище було зазначено, що
. Вище було зазначено, що ![]() -
це координати одиничного вектора
-
це координати одиничного вектора ![]() , а тому добуток
, а тому добуток 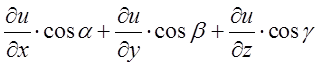 можна розглядати
як скалярний добуток одиничного вектора
можна розглядати
як скалярний добуток одиничного вектора ![]() на інший вектор з координатами
на інший вектор з координатами 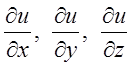 . Цей вектор і назвали градієнтом, а
позначили через
. Цей вектор і назвали градієнтом, а
позначили через ![]() або
або ![]() .
.
Означення. Градієнтом
функції ![]() називається вектор, проекціями якого
служать значення частинних похідних цієї
функції, тобто
називається вектор, проекціями якого
служать значення частинних похідних цієї
функції, тобто
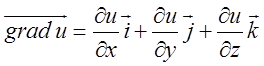 (11.4)
(11.4)
Підкреслимо, що проекції градієнта залежать від вибору точки Р (х,
у,z) і змінюються зі зміною координат цієї точки. Таким чином,
кожній точці скалярного поля, визначеного
функцією поля ![]() відповідає
визначений вектор – градієнт цієї функції. Відзначимо, що
градієнт лінійної функції
відповідає
визначений вектор – градієнт цієї функції. Відзначимо, що
градієнт лінійної функції ![]() є постійний вектор:
є постійний вектор: ![]() . Повертаючись до початку
цього пункту, ми бачимо, що
. Повертаючись до початку
цього пункту, ми бачимо, що 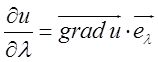 (11.5)
(11.5)
Таким чином. Похідна функції по даному напрямку дорівнює скалярному добутку градієнта функції на одиничний вектор цього напрямку.
З перетворення 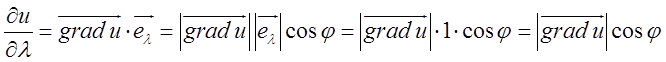 , ми бачимо що похідна функції по
даному напрямку дорівнює проекції градієнта функції на напрямок
диференціювання, де
, ми бачимо що похідна функції по
даному напрямку дорівнює проекції градієнта функції на напрямок
диференціювання, де ![]() -кут між вектором
-кут між вектором ![]() і променем
і променем ![]() .
.
Звідси
відразу випливає, що похідна по напрямку досягає найбільшого значення, коли ![]() , тобто при
, тобто при ![]() . Це
найбільше значення дорівнює
. Це
найбільше значення дорівнює ![]() .
.
Отже, ![]() є найбільше можливе значення похідної
є найбільше можливе значення похідної ![]() у даній
точці Р, а напрямок
у даній
точці Р, а напрямок ![]() збігається з напрямком променя, що виходить із точки Р, уздовж
якого функція міняється швидше всього, тобто напрямок градієнта є напрямок
найшвидшого зростання функції. Ясно, що в протилежному напрямку функція
збігається з напрямком променя, що виходить із точки Р, уздовж
якого функція міняється швидше всього, тобто напрямок градієнта є напрямок
найшвидшого зростання функції. Ясно, що в протилежному напрямку функція ![]() буде швидше всього спадати.
буде швидше всього спадати.
Доведемо тепер теорему, що встановлює зв'язок між напрямком градієнта функції і поверхнями рівня скалярного поля.
Теорема.
Градієнт функції ![]() у кожній точці
спрямований по нормалі до поверхні рівня скалярного поля,
що проходить через цю точку.
у кожній точці
спрямований по нормалі до поверхні рівня скалярного поля,
що проходить через цю точку.
Доведення. Виберемо довільну точку ![]() Рівняння
поверхні рівня, що проходить через точку
Рівняння
поверхні рівня, що проходить через точку ![]() запишеться
у вигляді
запишеться
у вигляді ![]() . Складемо рівняння нормалі до цієї поверхні в точці
. Складемо рівняння нормалі до цієї поверхні в точці![]() :
: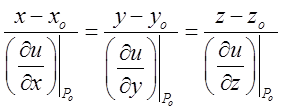 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.