Теорія поля. Скалярне поле. Поверхні рівня. Градієнт. Векторне поле і векторні лінії. Потік вектора через поверхню, страница 4

  то поле називається плоским. З плоскими полями дуже часто приходиться зустрічатися в механіці і гідродинаміці при вивченні плоских течій рідини, тобто таких течій, коли всі частки рідини рухаються паралельно деякій площині, причому швидкості часток, розташованих на одній і тій же прямій, перпендикулярній до цієї  площини однакові.                                  

 Розглянемо один дуже важливий приклад з механіки.

 Нехай тверде тіло обертається з постійною кутовою швидкістю  навколо якої-небудь осі. Знайдемо поле лінійних швидкостей точок цього тіла.                               

Як відомо з кінематики, лінійна швидкість  дорівнює векторному добутку:

   де   – вектор кутової швидкості (тобто вектор, відкладений на осі обертання і чисельно дорівнює величині кутової швидкості; цей вектор спрямований так, що, якщо дивитися з його кінця, обертання відбувається  проти годинникової стрілки), а – радіус-вектор точки М  тіла обертання щодо якої-небудь точки осі обертання. Вибравши цю нерухому точку за початок координат і, направивши вісь обертання по осі Оz (мал. 217), знайдемо проекції вектора.                                   

Так, як ,  то 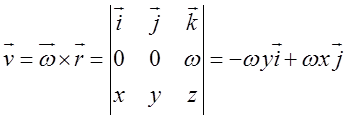. Таким чином, , і ми бачимо, що поле плоске.

О з н а ч е н н я. Векторною лінією векторного поля називається лінія, у кожній точці якої напрям дотичної збігається з напрямком вектора, що відповідає цій тічці.

.        Векторні лінії  в конкретних полях мають ясний фізичний зміст. Так, у полі швидкостей течії рідини векторні лінії суть лінії струму цієї рідини, тобто лінії, по яких рухаються частки рідини.

В електричному полі векторні лінії суть силові лінії цього поля. Наприклад, у полі точкового заряду такими лініями будуть промені, що виходять із заряду. Для магнітного поля векторними (силовими) лініями будуть лінії, які виходять з північного полюса і закінчуються в південному. Вивчення розположення силових линий  в електричних, магнітних і електромагнітних  – полях дуже важливе в фізиці.

Виведемо рівняння векторних ліній.

Нехай векторне поле визначене функцією .

Будемо шукати рівняння векторної лінії в просторі в параметричному вигляді, тобто вважаємо, що   векторна лінія має параметричні рівняння .

Проекції направляючого вектора дотичної до цієї лінії пропорційні похідним , а похідні пропорційні  диференціалам . Але ж вектор дотичної до кривої в даній точці співпадає з напрямком самого векторного поля . Записуючи умови паралельності вектора  і вектора, направленноро по дотичній до векторної лінії, одержимо

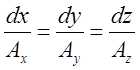.                                                                                                          (11.6)

Система рівнянь (11.6) представляє систему диференціальних рівнянь сімейства векторних ліній поля .

П.5. Знайти векторну лінію поля, яка проходить через точку ; .

Розв’язок. Скористаємось для знаходження векторних  ліній диференційними рівняннями 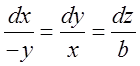 ; це система рівнянь. Представимо її у вигляді:

.

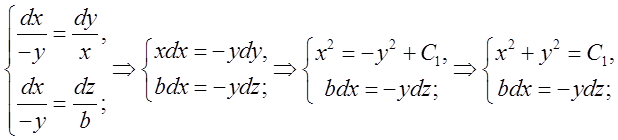Введемо параметр t і вважаємо . До цього нас штовхає не стільки наявність в першому рівнянні системи суми , як те, що при такій параметризації  в другому рівнянні замість трьох змінних  залишиться тільки дві . Після параметризації друге рівняння перетвориться в рівняння з відокремленими змінними і легко інтегрується.   .

Таким чином параметричні рівняння векторних ліній будуть мати вид

                                                                                            (*)

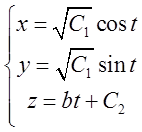Знайдемо значення параметра t, яке відповідає точці ; при  маємо

. Підставимо це значення параметра а також координати точки в  в (*) і отримаємо:

.

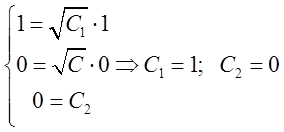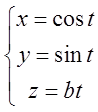Тому параметричне рівняння векторної лінії яка проходить через точку  буде гвинтова лінія   - це і є відповідь.

П.6. Проводячи досліди з магнітним полем провідника струму при вивченні шкільного курсу фізики, ви спостерігали як залізні опилки під дією магнітного поля провідника перпендикулярного до площини, на якій розсипані опилки утворювали концентричні кола, центром яких є точка перетину вісі провідника з площиною. Знайдемо тепер рівняння векторних ліній магнітного поля нескінченного провідника, по якому тече струмом величиною І.

Розв’язок: Систему координат виберемо так, щоб провідник співпав з напрямом вісі . Нехай струм має силу , тоді  для визначення вектора напруженості магнітного поля в точці , створюваного струмом,  застосуємо закон Біо-Савара у векторно-диференціальній  формі 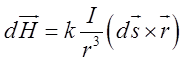, де  – вектор напруги магнітного поля, створеного струмом І, який проходить по дільниці-вектору   ;  – вектор, проведений з початку вектора   в точку ,  в якій знаходимо напруженість.