Теорія поля. Скалярне поле. Поверхні рівня. Градієнт. Векторне поле і векторні лінії. Потік вектора через поверхню, страница 6

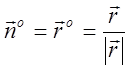Розв. Так, як нормаль  до сфери колінеарна радіусу-вектору, то можна взяти  .  Тому .

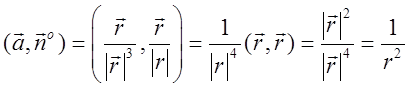Але на сфері S маємо , тому 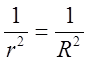. Шуканий потік К буде дорівнює

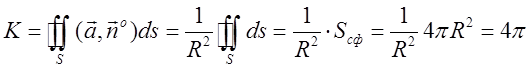. Відп..

П.9. Знайти потік вектора  через частину поверхні  відітнутої площиною z=2 Нормаль береться зовнішня стосовно області, обмеженої параболоїдом.

                      

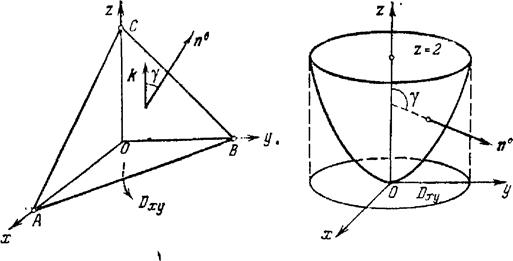
Рис. 18.                                           Рис. 19.

Розв. Дана поверхня (параболоїд обертання) проектується взаємно однозначно на площину хОу в коло (мал. 19). Знаходимо орт нормалі до поверхні S.

 ,

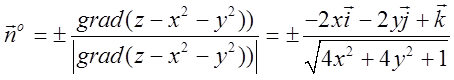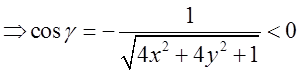
За умовою задачі нормаль утворює тупий кут  з віссю Оz, тому перед дробом ми взяли знак мінус 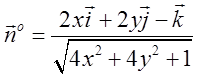.  Знаходимо скалярний добуток 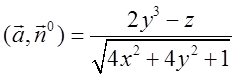, а потім за формулою (11.7) – потік. .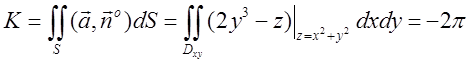

П.10. Знайти потік векторного полючи  через круг S, одержаний перетином  кулі  площиною            y=x. Узяти сторону круга  звернену до позитивного напрямку Ох.

Розв. Тому, що площина у=х перпендикулярна до координатної площини хОу, то круг S , що лежить на цій площині, проектується на площину хОу у відрізок довжиною 2R і, виходить, що порушується взаємна однозначність проектування. Треба проектувати на інші координатні площини, куди цей круг проектується областю, обмеженою еліпсом, з півосями R і . Проектуємо круг на площину xOz. Рівняння еліпса 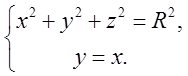 Виключаємо  з цієї системи змінну у (тому, що проектуємо на хОz)  .

З віссю Оу нормаль утворить тупий кут, тому беремо

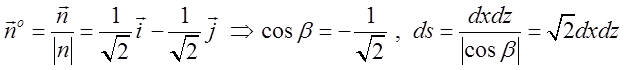 , . Потік шукаємо по формулі (11.7а), з огляду на те, що площа еліпса .У нас .    .

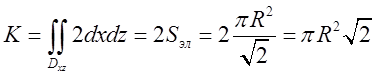П.11.  Обчислити потік вектора  через зовнішню сторону бічної поверхні кругового циліндра , обмеженою площинами z=0 і z=H (H>0).

Розв. Даний циліндр проектуєтьсяна площину хОу в лінію, а саме, в коло (мал. 21)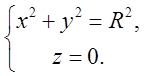  

Тому будемо проектувати циліндр на інші координатні площини, наприклад, на площину уОz. Тому що циліндр проектується на площину у0z не взаємно однозначно, то скористаємося властивістю аддитивности потоку вектора і представимо шуканий ноток К в виді суми потоків , де  — потік поля через частину  циліндра, розташовану в області, де у > 0, а  — потік цього ж поля через частину  циліндра, розташовану в області, де у < 0. На  маємо

 .

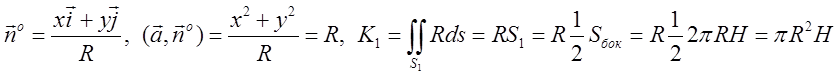На поверхні S₂ , аналогічно будемо мати

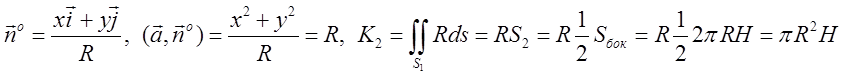
Загальний потік буде .

Запитання для самоперевірки.

!. Як задається скалярне поле в деякій області ?

2. Як знайти поверхні рівня скалярного поля?

3. Дайте визначення похідної скалярного поля  за напрямком .

4. Як знайти похідну скалярного поля  за напрямком ?

5. Як знайти напрямні косинуси променя ?

6. Дайте визначення  скалярного поля  в точці .

7. Як звязані між собою , де – одиничний вектор напрямку променя ?

8. Куди завжди напрямлений градієнт скалярного поля?

9. Який звязок між рівнінням нормалі до поверхні і  в т. ?

10. Чому дорівнюють: а)

11.Як задається векторне поле в деякій області ?

12. Коли векторне поле називають однорідним, плоским?

13. Що таке векторна лінія векторного поля?

14. Запишіть систему диференціальних рівнянь для знаходження векторних ліній

        векторного поля .

15. Дайте визначення потоку К векторного поля .

16. Як обчислити потік векторного поля .

17. Як обчислити потік векторного поля , коли проекція векторного поля

         на нормаль до поверхні є величина постійна?

                              Приклади для самостійного розв’язку

1. Обчислити потік векторного поля   через  верхню сторону  трикутника, вирізаного з площини площинами.Відп.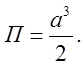

2. Обчислити потік векторного поля  через зовнішню сторону параболоїда  обмеженого площиною .Відп.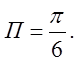

3. Обчислити потік векторного поля через бічну поверхню кругового циліндра  обмежену площинами . Відп.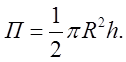

4. Обчислити потік векторного поля  через верхню сторону кркга, що вирізується конусом  на площині  Відп.

5. Обчислити   потік   векторного   поля   через зовнішню сторону параболоїда , розташовану в першому октанті. Відп.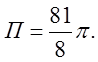

6. Обчислити потік векторного поля

через частину площини z=0, обмежену колом  в напрямку орта . Відп.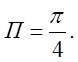

7. Обчислити потік векторного поля  через повну поверхню конуса , обмежену площиною . Відп.

8. Обчислити потік векторного поля  через замкнуту поверхню, обмежену параболоїдом  і площиною z= 0. Відп.

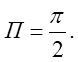
9. Обчислити потік векторного поля  через повну поверхню піраміди, обмеженої площинами . Відп.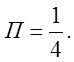

10. Обчислити потік векторного поля  через сферу . Відп.