Теорія поля. Дивергенція векторного поля. Циркуляція і ротор векторного поля. Оператори Гамільтона і Лапласа та дії з ними

Лекція 12

Теорія поля

План:

 12.1. дивергенція векторного поля.

 12.2.Циркуляція і ротор векторного поля.

 12.3. Оператори Гамільтона і Лапласа та дії з ними.

 12.4. запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1. Якщо кожна частинка деякого об’єму V випромінює (або має якусь іншу характеристику), і величина загального випромінювання (чи якоїсь іншої характеристики) дорівнює К, то щоб знайти величину випромінювання (чи якоїсь іншої характеристики) на одиницю об’єму треба К розділити на V. Це буде потужність випромінювання (чи якоїсь іншої характеристики) з даного об’єму. Це поняття використовується при введенні понять дивергенції і ротору векторного поля.

2. Векторний добуток  двох векторів  виражається через визначник 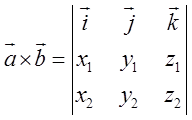, який розкривається за першим рядочком, тобто

.

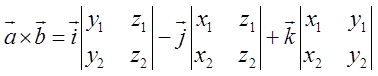2. Якщо для  другі змішані похідні 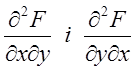неперервні, то вони рівні між собою, тобто  .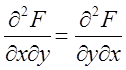

12.1. Дивергенція векторного поля     

 Розглянемо деяку точку Р векторного поля  і оточимо її замкнутою поверхнею S, яка цілком міститься в полі. Обчислимо потік вектора через поверхню S і візьмемо, відношення цього потоку до об’єму V області , обмеженою поверхнеюS:      .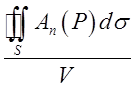

В полі швидкостей рідини це відношення визначає кількість рідини, що виникає в одиницю часу в області , в  одиниці об'єму, тобто воно визначає  середню об’ємну   потужність джерела; якщо потік зсередини поверхні S менше нуля, то відповідно говорять про середню об’ємну потужність стоку.

Знайдемо тепер границю цього відношення при  .

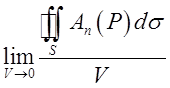Якщо ця границя позитивна, то точка Р називається джерелом, а якщо негативна, то стоком. Сама величина границі характеризує потужність  джерела  чи стоку. У першому випадку в любому нескінченно малому об’ємі, що оточує точку Р, рідина з’являється, а в другому випадку зникає. Ця границя і називається д и в е р г е н ц і є ю або

 р о з б і ж н і с т ю векторного поля в точці Р.

Означення. Дивергенцією або розбіжністю векторного поля  у точці Р називається границя відношення потоку вектора через поверхню, що оточує точку Р до об’єму, обмеженому цією поверхнею, за умови, що уся поверхня стягується в точку Р.

Дивергенцію поля позначають символом . Таким чином

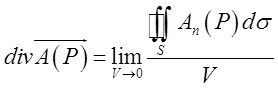,                                                                                    (12.1)

де границя обчислюється при умові, що поверхня S стягягується  в точку Р.

Ми доведемо зараз, що при прийнятих нами умовах неперервності функцій  і їхніх похідних дивергенція поля існує в будь-якій його точці (тобто існує зазначена границя), а також знайдемо її величину. Підкреслимо відразу, що дивергенція векторного поля є величина скалярна.

Теорема. Дивергенція  векторного поля  виражається формулою 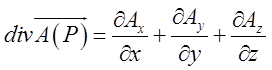       ,                                                         (12.2)

де значення частинних похідних беруться в точці Р.

Доведення. За формулою Остроградского (10.17)потік вектора К можна представити у вигляді

==          

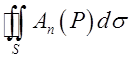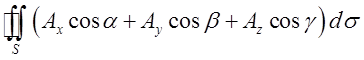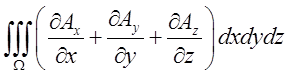
Потрійний інтеграл по теоремі про середє значення  дорівнює добутку об'єму V на значення підінтегральної функції в деякій точці   області , тобто

=.

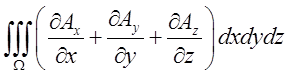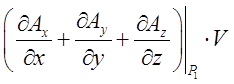Якщо область  стягається в точку Р, то точка  прямує до точки Р, і ми одержуємо

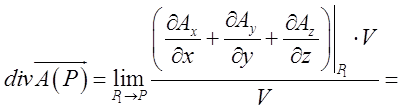
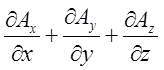
що і  потрібно було довести.

Користаючись виразом для дивергенції, теорему Остроградского можна сформулювати у векторній формі:

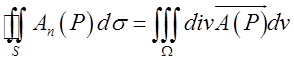                                                                                             (12.3)

Потік вектора зсередини замкнутої поверхні дорівнює потрійному інтегралу по об’єму, обмеженому цією поверхнею, від  дивергенції  поля.         

Стосовно до поля швидкостей течії рідини векторна форма теореми Остроградского  виражає той очевидний факт, що потік рідини через, поверхню дорівнює сумарній потужності всіх джерел і стоків, тобто кількості рідини, що виникає в розглянутій області за одиницю часу. Якщо потужність стоків більша, ніж джерел, то рідина в об’ємі зникає. Якщо дивергенція в усіх точках дорівнює нулю, то дорівнює нулю і потік через будь-яку замкнуту поверхню.

П.1. Обчислити , де  – радіус вектор точки .

Розв. Очевидно, що  і тому за формулою (12.2) маємо: 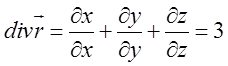. Звідси випливає, що кожна точка заданого  поля є як би джерелом постійної потужності. Користуючись  векторною формою теореми Остроградского, відразу одержуємо, що потік радіуса-вектора через будь-яку замкнуту поверхню дорівнює потроєному об’єму, обмеженому цією поверхнею: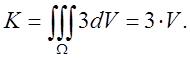

П.2. Обчислити 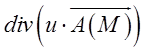, де  – скалярна функція, а  – векторна функція (векторне поле).