Теорія поля. Дивергенція векторного поля. Циркуляція і ротор векторного поля. Оператори Гамільтона і Лапласа та дії з ними, страница 2

Розв. Використовуючи (12.2), матимемо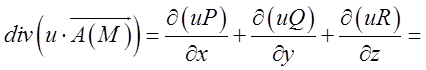 

=

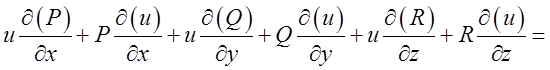
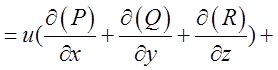
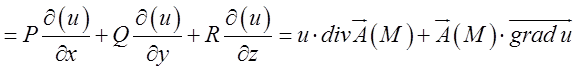. Це і є відповідь.

П.3. Обчислимо дивергенцію поля лінійних швидкостей  тіла, що обертається.

Розв. Поле швидкостей цього тіла буде плоске. Ми його обчислили в попередній лекції . Як бачимо, , а тому.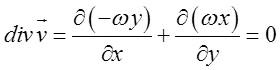

Якщо уявити  рідину, що обертається, як тверде тіло, то ясно, що в такому потоці немає ні джерел, ні стоків.

П.4. Знайти дивергенцію векторного поля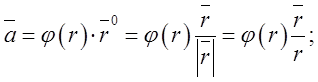 

де  - віддаль від точки  до початку координат,   - радіус вектор цієї точки,   – одиничний вектор напрямку вектора .

Розв’язок: Згідно формули (*) маємо:    .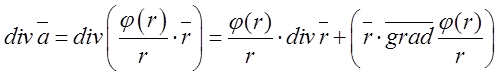

З попереднього  прикладу 1   а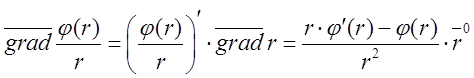 

А тому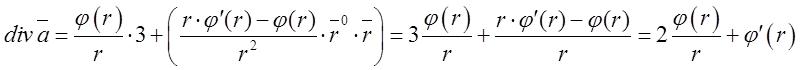

Відповідь: .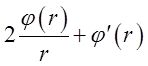

 При обчисленні дивергенції зручно  користуватися  її властивостями одну з яких ми вже довели (приклад 2):.

Наступною властивістю дивергенції є її лінійність: ,  яка дуже легко доводиться.

12.2. Циркуляція і ротор векторного поля

             Нехай векторне поле утворене вектором .

Візьмемо в цьому полі деяку лінію L і виберемо на ній визначений напрям. Позначимо через  вектор, що має напрямок дотичної до лінії і по модулю рівний диференціалу довжини дуги. Напрямок дотичної вважається; співпадаючим з обраним напрямком на лінії. Тоді

Розглянемо криволінійний інтеграл по лінії L від скалярного добутку векторів :

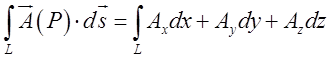                                                                                       (12.4)

  З цим інтегралом ми вже знайомі з лекції 10 і, як ми це бачили, в  силовому  полі інтеграл, (12.4) виражає роботу при переміщенні матеріальної точки вздовж лінії L .

Якщо  – довільне векторне поле, а L – замкнутий контур, то інтеграл (12.4) носить спеціальну назву – ц и р к у л я ц і я    вектора.

Означення. Циркуляцією вектора  уздовж замкнутого контуру L називається криволінійний інтеграл по цьому контурі від скалярного добутку вектора  на вектор дотичної до контуру L. Позначатимемо циркуляцію через  Ц.

Тому, що скалярний добуток , де – проекція вектора поля на напрямок дотичної, а  – диференціал довжини дуги, то циркуляцію можна записати у вигляді криволінійного інтеграла, по довжині дуги кривої: .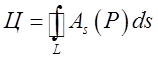

У довільному векторному полі циркуляція є деяке число, що залежить від контуру L. Нехай, наприклад, у полі є замкнуті векторні лінії. Виберемо лінію інтегрування, що збігається з векторною лінією. Тоді , у з’вязку з тим, що кут між векторами  дорівнює нулю одержимо: 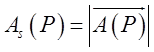 і, циркуляція, тобто   як інтеграл від додатньої функції, є число напевно позитивне. Якщо напрямок інтегрування змінити на протилежний, то циркуляція стане негативної. Якщо L не є векторною лінією, то циркуляція буде тим більшою, чим менший кут між вектором поля   і напрямком відповідних дотичних .

П.4.Обчислити циркуляцію поля  вздовж еліпса .

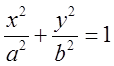Розв. Скористаємось формулою (12.4) 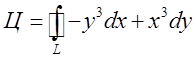. Зводячи цей інтеграл до звичайного, рівняння контура запишемо в параметричному виді 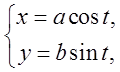 при .

Підставимо 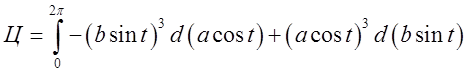 = =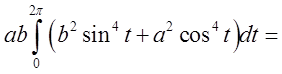 = =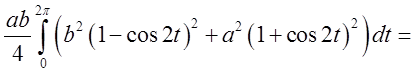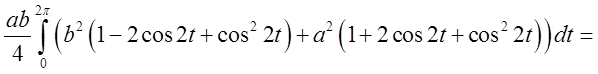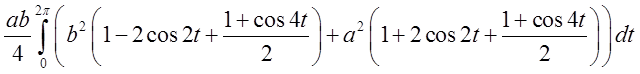.  Очевидно, що 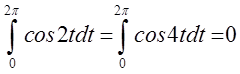, а тому 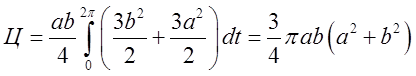. Це і є відповідь.

 П.5.Обчислимо циркуляцію вектора поля лінійних швидкостей тіла, яке  обертається з швидкістю  вздовж контура L , розташованого повністю в площині П.

Розв. З вигляду векторного поля бачимо, що  – кутова швидкість, Оz – вісь обертання (рис.12. 1). Нормаль  до площини П утворює з осями координат кути . Напрямок обходу контуру L і напрямок нормалі  погоджені між собою так, як у теоремі Стокса

       Рис.12.1.                 Відповідно до визначення циркуляція дорівнює

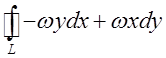. Застосуємо для обчислення цього інтегралу теорему Стокса: 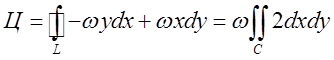, де С – область, обмежена контуром L. Інтегрування ведеться по верхній строні площини П і тому . У нас . Так як С частина площини П то циркуляция дорівнює 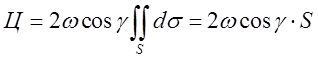, де S – площа області С, обмеженої контуром L. Зауважимо, що  – проекція вектора  на напрямок вектора . Тому остаточно вираз для циркуляції прийме вигляд

(Якщо L – коло радіуса R, то циркуляція дорівнює ).