а)![]() =
=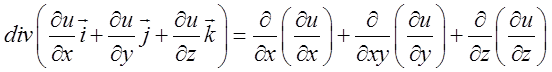 =
=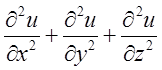 .
.
Вираз 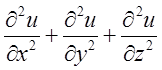 називається
оператором Лапласа від функції
називається
оператором Лапласа від функції ![]() , позначається
, позначається ![]() . Дивергенцію від градієнта можна виразити
двічі застосовуючи оператор Гамільтона
. Дивергенцію від градієнта можна виразити
двічі застосовуючи оператор Гамільтона
![]()
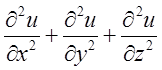 .
(12.14)
.
(12.14)
Як ми бачимо ![]() це
зв’язок між операторами Гамільтона і Лапласа.
це
зв’язок між операторами Гамільтона і Лапласа.
б) ![]() (12.15)
(12.15)
Співвідношення це перевіряється зовсім просто, треба за
визначенням знайти ротор від градієнта, тобто від поля 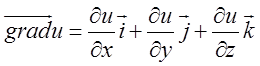 . Тут
. Тут 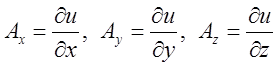 і тому:
і тому:
![]()
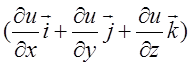 =
=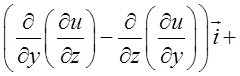
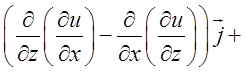
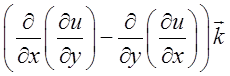 .
Кожна дужка у виразі для ротора представляє в цьому випадку різницю других
змішаних похідні функції
.
Кожна дужка у виразі для ротора представляє в цьому випадку різницю других
змішаних похідні функції ![]() , що відрізняються лише
порядком диференціювання, а тому всі координати вектора рівні нулю.Це
співвідношення легко запам'ятовується, якщо записати його за допомогою
набла-вектора:
, що відрізняються лише
порядком диференціювання, а тому всі координати вектора рівні нулю.Це
співвідношення легко запам'ятовується, якщо записати його за допомогою
набла-вектора: ![]() ,
,
тому,що векторний добуток однакових «векторів» дорівнює нулю.
в) ![]() . (12.15)
. (12.15)
Утворимо дивергенцію від ![]()
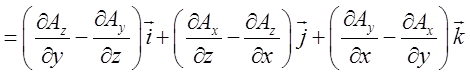 .
.
![]()
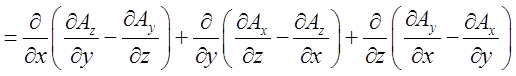 =
=
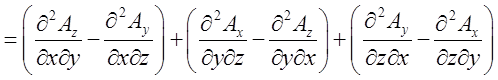 ,
,
що в силу рівності других змішаних похідних дорівнює нулю. Якщо записати доводжуване співвідношення за допомогою набла-вектора:
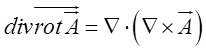 , то одержимо змішаний
добуток трьох «векторів», з яких два вектори однакові. Але такий добуток
дорівнює нулю.
, то одержимо змішаний
добуток трьох «векторів», з яких два вектори однакові. Але такий добуток
дорівнює нулю.
Інші дві векторні операції другого порядку: ![]() і
і ![]() зустрічаються
рідше, їх вираження через оператори Гамільтона і Лапласа дуже громіздке. При
виконанні цих операцій в кожному конкретному випадку треба діяти за
означенням. Ми не будемо записувати їхнього вираження через проекції вектора
зустрічаються
рідше, їх вираження через оператори Гамільтона і Лапласа дуже громіздке. При
виконанні цих операцій в кожному конкретному випадку треба діяти за
означенням. Ми не будемо записувати їхнього вираження через проекції вектора ![]() , а тільки вкажемо на зв'язок між ними:
, а тільки вкажемо на зв'язок між ними:
![]() =
=![]() . (12.16)
. (12.16)
Для доведення (12.16) розпишемо внутрішні
оператори, вважаючи, що ![]() .
.
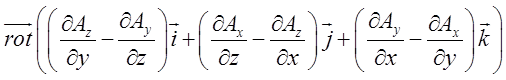 =
=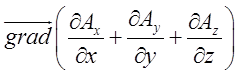 –
–
–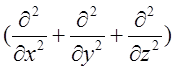
![]() .
Так як (12.16) векторна рівність, то треба довести рівність відповідних
координат (проекцій на координатні вісі) зліва і справа. Обчислимо координати
(проекції) на вісь Ох, тобто
.
Так як (12.16) векторна рівність, то треба довести рівність відповідних
координат (проекцій на координатні вісі) зліва і справа. Обчислимо координати
(проекції) на вісь Ох, тобто ![]() =
=![]() .
.
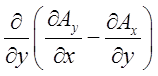 –
–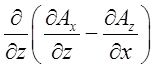 =
=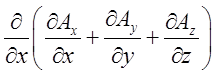 –
–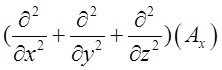 .
.
Розкриваючи дужки, переконуємось в рівності проекцій на вісь Оz правої і лівої частини. Аналогічно переконуємося і в рівності проекцій на інші вісі.
1. Дати визначення дивергенції векторного поля. Вивести формулу для вираження дивергенції.
2. Сформулювати у векторній формі теорему Остроградского і вказати її фізичний зміст.
3. Що називається циркуляцією вектора?
4. Вивести формулу для границі відношення циркуляції вектора по плоскому контурі L до площі, обмеженої цим контуром.
5. Дати визначення ротора векторного поля. Сформулювати у векторній формі теорему Стокса.
6. Чому дорівнює ротор вектора напруженості магнітного поля нескінченно довгого провідника, по якому тече струм І ?
7.Сформулювати правила дій з оператором Гамильтона.
8. Перелічити всі можливі диференціальні векторні операції другого порядку.
9. Чому дорівнюють: ![]() ,
, ![]() ,
, ![]() ?
?
Розвязати самостійно
12.1. Знайти дивергенцію векторного поля ![]() , де
, де ![]() –
постійний вектор
–
постійний вектор![]() .
.
Відп. 0.
12.2. Знайти дивергенцію векторного поля ![]() , де
, де ![]() –
постійний
–
постійний
вектор![]() .
Відп. 0.
.
Відп. 0.
12.3. При якій функції ![]() дивергенція
поля
дивергенція
поля ![]() буде дорівнювати z?
буде дорівнювати z?
Відп. ![]() .
.
12.4. Обчислити циркуляцію Ц вектора ![]() вздовж лінії
вздовж лінії 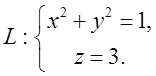 Відп.
Відп. ![]() .
.
12.5. Обчислити циркуляцію Ц вектора ![]() вздовж лінії
вздовж лінії 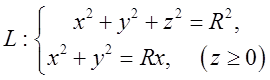 . Відп.
. Відп.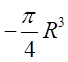 .
.
12.6. Знайти ротор слідуючих векторних полів:
а) ![]() .
Відп.
.
Відп.![]() .
.
б) ![]() . Відп.
. Відп.![]() .
.
в) 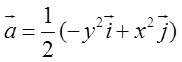 .
Відп.
.
Відп.![]() .
.
12.7. Яка повинна бути функція ![]() , щоб
, щоб ![]() ?
?
Відп.![]() .
.
12.8. Застосовуючи теорему Стокса, обчислити
циркуляцію вектора ![]() по контуру
по контуру 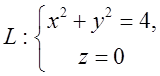 . Відп.
. Відп.![]() .
.
12.9. Застосовуючи теорему Стокса, обчислити
циркуляцію вектора ![]() по контуру
по контуру 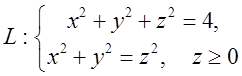 . Відп.–
. Відп.–![]() .
.
12.10. Застосовуючи теорему Стокса, обчислити
циркуляцію вектора ![]() по контуру утвореному перетином
площини
по контуру утвореному перетином
площини ![]() з координатними площинами. Відп.4/3.
з координатними площинами. Відп.4/3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.