Теорія поля. Дивергенція векторного поля. Циркуляція і ротор векторного поля. Оператори Гамільтона і Лапласа та дії з ними, страница 4

Проекція  цього вектора на будь-який напрямок є границя відношення циркуляції вектора поля по, контуру, що лежить у площині, яка проходить через точку Р і для якої вектор  є нормаллю, до площі, обмеженої цим контуром. Ця границя буде найбільшою у тому випадку, коли напрямок нормалі збігається з напрямком .

За допомогою визначення ротора теорему Стокса можна подати у векторній формі:

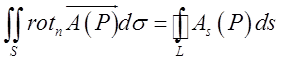                                                                                    (12.6)

Потік ротора поля через поверхню S дорівнює циркуляції вектора по границі цієї поверхні.

Звідси випливає, що якщо дві поверхні  мають одну і ту ж границю L, то потоки ротора через ці поверхні рівні між собою.

Наведемо дві властивості ротора поля.

1. Перша властивість виражає лінійність ротора і її доведення очевидне.

                                                  (12.7)

2. Доведемо ще, що якщо – скалярна функція, а – векторна, то

                                                                                        (12.8)

Щоб довести (12.8) розпишемо  згідно з (12.5).

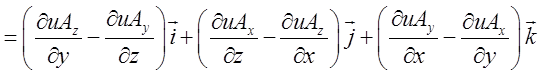=++=. Перетворимо окремо кожну з координат. 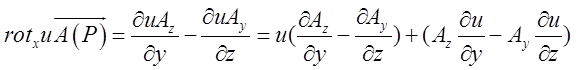. Аналогічно ,.

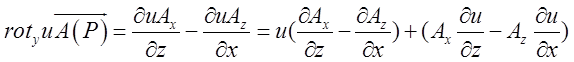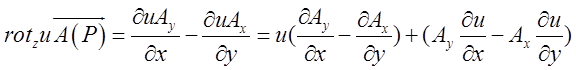Підставимо знайдені координати в початковий вираз, перегрупуємо і з трьох доданків винесемо за дужки спільний множник . В дужці одержимо . Три дужки, які залишились -  це розкритий визначник 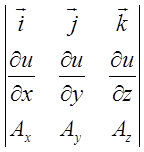, який дорівнює  і властивість доведена.

П.6. Обчислити ротор векторного поля:  

Розв’язок: Використаємо формулу (12.5)

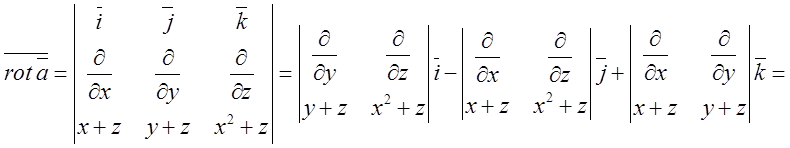
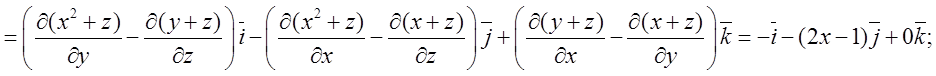
Відповідь: .

П.7. Знайти ротор вектора напруженості магнітного поля нескінченно довгого провідника по якому тече струм силою І.

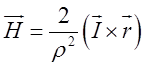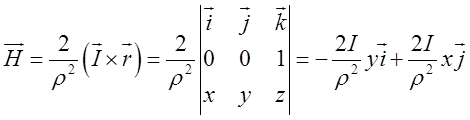
Розв. Введемо систему координат, спрямувавши вісь провідника вздовж вісі Оz. Як відомо з фізики, вектор напруженості магнітного поля, створеного струмом, дорівнює . Завдяки обраній системі координат ми можемо, знаючи величину струму І, знайти . Так як напрямним одиничним вектором для напрямку провідника є орт  (вісь провідника співпадає з віссю Оz), то .   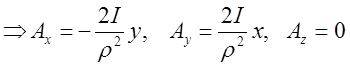 , де . Знаходимо ротор вектора напруженості, застосовуючи (12.5).

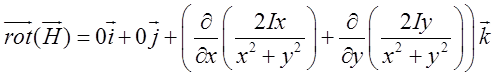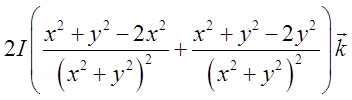==0.

Звідси бачимо, що=0 всюди крім вісі Оz, де він не визначений (при х=у=0 знаменник обертається в нуль). А це значить, що магнітне поле вектора  всюди є безвихрове крім точок , які знаходяться на вісі провідника струму.  

12.3. Оператори Гамільтона і Лапласа та дії з ними

Розглянуті вище основні поняття векторного аналізу: г р а д і є н т,  д и в е р г е н ц  і я       і    р о т о р – зручно представляти за допомогою символічного в е к т о р а   («набла-вектор»).

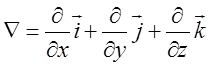                                                                                                           (12.9)

Розглянемо правила застосування  цього вектора, який часто називають оператором Гамільтона:

1. Простий добуток цього оператора на скалярну функцію  дає градієнт цієї функції

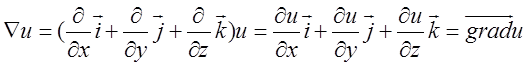.                                (12.10)

2. Скалярний добуток набла-вектора  на векторну функцію  дає дивергенцію цієї функції:

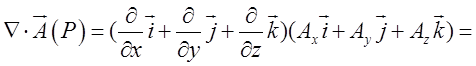
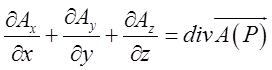      (12.11)

 3. Векторний добуток   набла-вектора  на векторну функцію    дає ротор цієї функції:

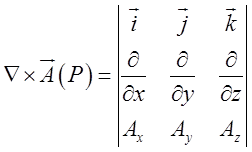
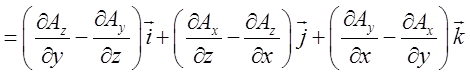                (12.13)

Таким чином, дії з набла-вектором (оператором Гамільтона) здійснюються за звичайними правилами дій векторної алгебри, а потім множення наприклад,  на скалярну функцію  , заміняється похідною цієї функції по х.

Операції знаходження градієнта, дивергенції і ротора будуть, векторними диференціальними операціями першого порядку. У них беруть участь тільки перші похідні від скалярних функцій або тільки один раз застосовують оператор .

Перейдемо тепер до векторних диференціальних операцій другого порядку.

Якщо у нас є скалярне поле  і ми знайшли градієнт  цього поля , то поле градієнта є векторним полем і ми можемо шукати його дивергенцію і ротор: і  .

Якщо у нас є  векторне поле  то ми можемо знайти його дивергенцію і ротор тобто векторне поле породжує два поля: скалярне поле дивергенції  і векторне поле ротора  . Отже, ми можемо знаходити градієнт першого поля : і дивергенцію та ротор другого поля   і .  Усього ми маємо п'ять векторних диференціальних операцій другого порядку. Розглянемо їх.