Теорія поля. Дивергенція векторного поля. Циркуляція і ротор векторного поля. Оператори Гамільтона і Лапласа та дії з ними, страница 3

З цієї формули випливає, що якщо площину П повертати, тобто змінювати кут , то величина циркуляції буде мінятися. Найбільшою вона буде, коли , тобто коли площина П паралельна площині Оху і нормаль  до неї  паралельна вектору кутової швидкості  . Якщо ж  нормаль до площини перпендикулярна до вектора, то циркуляція дорівнює нулю

Зрозуміло також, що якщо перемінити сторону площини П, то вектор  змінить напрямок і проекція  стане від’ємною. Тому і циркуляція також буде величиною від’ємною.

Установимо тепер фізичний зміст циркуляції вектора  у випадку, коли  – поле швидкостей течії рідини. Приймемо для простоти, що контур L – коло, розташоване в деякій площині. Уявимо, що коло обмежує  колесо з радіальними лопатками, яке може обертатися навколо осі, що проходить  через його центр перпендикулярно до його площини. Це може бути, наприклад, різновидність турбіни. Якщо циркуляція  дорівнює нулю, то коллесо буде залишатися нерухомим: сили, що діють на лопатки, врівноважують одна одну. Якщо циркуляція не дорівнює нулю, то колесо буде обертатися, тим швидше, чим більша величина циркуляції. Якщо, наприклад, рідина обертається, як тверде тіло, навколо вісі Оz і якщо вісь колеса збігається з напрямком вісі обертання, то, як ми тільки що бачили, циркуляція дорівнює , де S – площа колеса.Таким чином, відношення циркуляції до площі колеса дорівнює подвоєній кутовій швидкості і не залежить від розмірів колеса.

Якщо вісь колеса нахилити до вісі Оz, то зазначене відношення зменшиться і стане рівним , де– проекція вектора  на напрямок вісі колеса. Нарешті, якщо вісь колеса стане перпендикулярною до вісі обертання рідини, то колесо буде нерухомим.

У випадку довільного векторного поля відношення циркуляції по плоскому контуру до площі S, обмеженої цим контуром, буде величиною з м і н н о ю. Щоб охарактеризувати обертальну властивість векторного поля в якій-небудь його точці Р, розглянемо границю відношення циркуляції по плоскому контуру L, що оточує точку Р, до площі S, обмеженої цим контуром, за умови, що контур L стягyється в точку Р, залишаючись в одній і тій же площині, тобто  .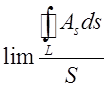

Доведемо, що ця границя буде залежати тільки від обраної точки Р і від напрямку нормалі  площини в якій лежить контур L. Після  того, як нормаль проведена до визначеної сторони площини, – напрямок обходу контуру L  цілком визначено: а саме обхід відбувається проти годинникової стрілки, якщо дивитися з кінця вектора нормалі. Щоб обчислити вище написану границю, перетворимо вираз для циркуляції, скориставшись формулою Стокса (10.10):

 =, 

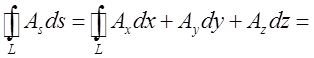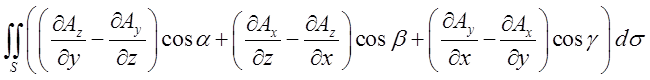де - напрямні косинуси нормалі , а S – область, обмежена контуром L. Останній інтеграл по теоремі про середнє значення дорівнює добутку значення підінтегральної функції в деякій точці , області S на величину S площі цієї області. При стягуванні контуру L в точку P (при цьому ) значення підінтегральної функції буде прямувати до її значення в точці Р. Тому, після скорочення на S в правій частині, одержимо

=,

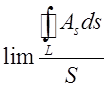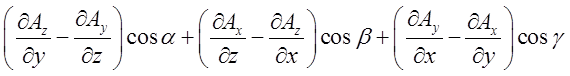де значення всіх частинних похідних беруться а точці Р. Права частина рівності, скалярний добуток двох векторів: одиничного, вектора   – нормалі до площини, у якій лежить контур L, і вектора, проекції  якого дорівнюють різницям, що стоять в дужках. Цьому вектору дали назву: ротор або вихор векторного поля і позначили.

О з н а ч е н н я.Ротором векторного поля      називається вектор             

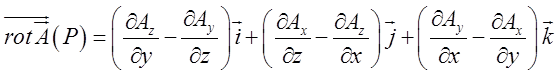                                                            (12.5)

Представимо цей вектор через визначник, зробивши деякі припущення з приводу його розкриття. 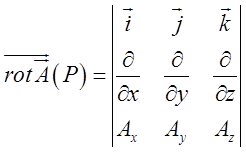.                                                                             (12.5а)

При розписуванні цього визначника за першим рядочком,  вираз типу 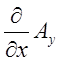 розглядається не як добуток, а як знаходження похідної по змінній х від функції . Таким чином, при цій домовленості (12.5) і (12.5а) це один і той же вираз для  вектора ротора поля.