Системи звичайних диференціальних рівнянь. Теорія лінійних систем

Розділ 1.

СИСТЕМИ ЗВИЧАЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ.

ТЕОРІЯ ЛІНІЙНИХ СИСТЕМ

1.1. Загальні поняття

При розв'язанні різних задач прикладного характеру доводиться знаходити відразу кілька невідомих функцій, що залежать від одного аргументу, що входять у кілька рівнянь, тобто приходиться мати справу із системою рівнянь.

Системою диференціальних рівнянь називається система, що зв'язує незалежну змінну , невідомі функції цієї змінної  й похідні цих функцій по незалежній змінній. Загальний вид системи диференціальних рівнянь такий:

                        (1.1)

Порядком системи (1.1) називають число , рівне .

Розв'язанням системи (1.1) на інтервалі  називають сукупність функцій:

,                                               (1.2)

підстановка яких разом з їхніми похідними в систему (1.1) перетворює кожне рівняння системи в тотожність. При цьому припускається, що число рівнянь  системи (1.1) дорівнює числу невідомих функцій , причому якщо , те така система стає невизначеною.У цьому випадку можна вибрати довільно  шуканих функцій (аби тільки вони були потрібне число раз диференційовані) і залежно від них знаходити інші  функцій. Якщо ж число шуканих функцій  менше числа рівнянь системи , то ця система може опинитися неспільною, тобто не має жодного розв'язання.

Розв’язав систему (1.1) щодо старших похідних всіх функцій, що входять у цю систему (передбачається виконання умов теореми існування неявних функцій), одержимо:

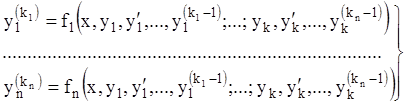.                                      (1.3)

Систему виду (1.3), розв’язану щодо своїх старших похідних, називаютьканонічною. Канонічну систему називають нормальною, якщо в лівих частинах знаходяться похідні тільки першого порядку, а праві зовсім не містять похідних, тобто

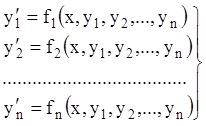.                                                           (1.4)

Очевидно, що порядок нормальної системи (1.4) дорівнює числу рівнянь у неї вхідних, тобто .

Якщо праві частини системи (1.4) залежать лінійно від шуканих функцій , тобто, якщо система (1.4) має вигляд:

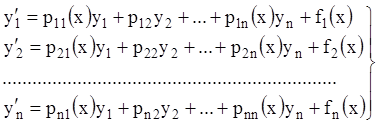,                                           (1.5)

де  й   – задані неперервні в розглянутій області функції, то її називають лінійною системою. Якщо , то систему (1.5) називають лінійною системою диференціальних рівнянь із постійними коефіцієнтами.

Якщо праві частини системи (1.4) не залежать явно від незалежної змінної , тобто система має вигляд:

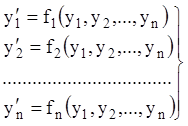,                                                            (1.6)

то її називають автономною або стаціонарною.

Дві системи диференціальних рівнянь називаються еквівалентними, якщо вони мають ті самі розв'язки. Виявляється, що будь-яку канонічну систему (1.3) завжди можна перетворити в еквівалентну нормальну систему, причому порядок цих систем буде тим самим. Для цього досить кожну похідну невідомих функцій, за винятком найбільших, замінити новою невідомою функцією. Наприклад, канонічна система:

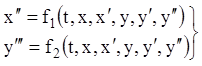
після введення нових невідомих функцій  приводиться до нормальної системи:

.

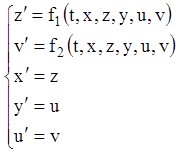У зв'язку з тим, що будь-яку канонічну систему завжди можна перетворити в еквівалентну нормальну систему, далі будемо розглядати тільки нормальні системи.

Розглянемо задачу, що приводить до системи диференціальних рівнянь: визначити траєкторію руху снаряда, викинутого з початковою швидкістю  під кутом  до обрію, вважаючи опір повітря пропорційним швидкості руху.

Розв'язання. За початок координат візьмемо точку вильоту снаряда. Рівняння руху будуть:

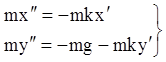.                                                           (1.7)

(На снаряд діє його сила ваги , її складова на осі  дорівнює нулю, тому що сила ваги перпендикулярна до осі ). Якщо ж зневажити опором повітря, то система (1.7) запишеться:

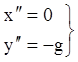.                                                                    (1.8)

Тобто задача, навіть при дуже спрощених умовах, зводиться до розв'язання системи двох рівнянь (1.8). Вирішимо її, інтегруючи рівняння:

.

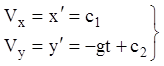У початковий момент часу  компоненти швидкості будуть: , . Тоді  й  і система запишеться

.

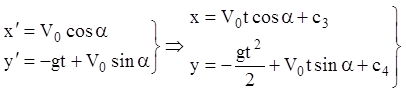Тому що при  , то .

Остаточний рух:

.

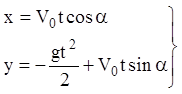Крім параметра , знайдемо траєкторію руху:

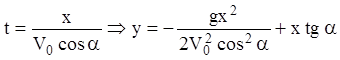 — парабола.

Дистанція польоту снаряда знаходиться з рівняння :

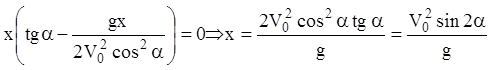
( – вихідна точка).

Легко бачити, що максимальна дистанція буде при стрілянині під кутом 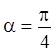 (у дійсності цей кут приблизно дорівнює ).

1.2 Геометричне й механічне тлумачення нормальної системи

Відомо, що рівняння першого порядку  задає на площині  деяке поле напрямків, і що напрямок дотичній у будь-якій точці інтегральної кривої збігається з напрямком поля в цій точці. Аналогічне геометричне тлумачення можна дати й нормальній системі (1.4). Будемо розглядати  як координати точки в  - мірному просторі . Тоді розв'язанню (1.2) відповідає деяка крива в  - мірному просторі. Вона називається інтегральної кривої системи (1.4). З'ясуємо геометричний зміст інтегральних кривих.

Нехай праві частини системи (1.4) визначені та кінцеві в деякій області  зміни змінних . Проведемо в кожній точці області  відрізок, напрямні косинуси якого пропорційні одиниці й значенням правих частин системи (4) у цій точці й назвемо множину цих відрізків полем напрямків.