 . (1.51)
. (1.51)
Приклад.
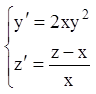 .
.
Розв'язання. Розв’язуємо перше рівняння системи:
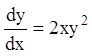 ;
; 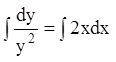 ;
; 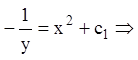
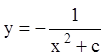 .
.
Розв’язуємо друге рівняння: 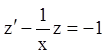 – лінійне рівняння першого
порядку. Розв’язав його одержуємо
– лінійне рівняння першого
порядку. Розв’язав його одержуємо ![]() .
.
Відповідь: 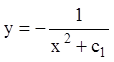 ,
, ![]() .
.
Приклад.
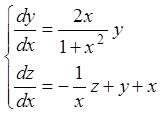
Розв'язання. З першого рівняння 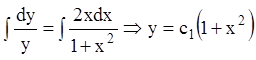 .
.
Підставляючи в друге рівняння, одержуємо 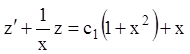 – лінійне рівняння першого порядку.
Розв’язав його, одержуємо
– лінійне рівняння першого порядку.
Розв’язав його, одержуємо 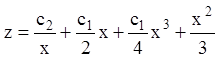 .
.
Відповідь: ![]() ,
, 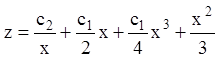 .
.
Один з основних методів інтегрування систем диференціальних рівнянь полягає в наступному: з рівнянь системи (1.16) і з рівнянь, що утворюються диференціюванням рівнянь системи, виключають всі невідомі функції, крім однієї, для визначення якої одержують одне диференціальне рівняння більше високого порядку. Інтегруючи отримане рівняння, знаходять одну з невідомих функцій, а інші невідомі функції знаходять із вихідних рівнянь і рівнянь, що вийшли в результаті їхнього диференціювання.
Нехай дана нормальна система ![]() диференціальних рівнянь
виду:
диференціальних рівнянь
виду:
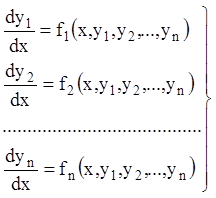 ,
(1.52)
,
(1.52)
у якій всі функції ![]() мають неперервні частинні похідні до
мають неперервні частинні похідні до ![]() -го порядку включно по всіх своїх
аргументах. Покажемо, що одна з невідомих функцій, наприклад
-го порядку включно по всіх своїх
аргументах. Покажемо, що одна з невідомих функцій, наприклад ![]() , що входить до складу розв'язання
, що входить до складу розв'язання ![]() системи (1.52), задовольняє деякому рівнянню
системи (1.52), задовольняє деякому рівнянню
![]() -го порядку. Підставивши в систему (1.52)
деяке її розв'язання
-го порядку. Підставивши в систему (1.52)
деяке її розв'язання ![]() , обернемо всі рівняння системи в
тотожності. Тоді, продиференціював першу тотожність по
, обернемо всі рівняння системи в
тотожності. Тоді, продиференціював першу тотожність по ![]() ,
одержимо:
,
одержимо:
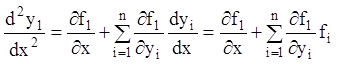 .
(1.53)
.
(1.53)
Позначивши праву частину останньої тотожності через ![]() , одержимо:
, одержимо:
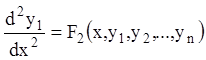 .
(1.54)
.
(1.54)
Диференціюючи (1.54), одержуємо:
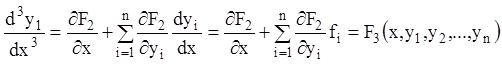 (1.55)
(1.55)
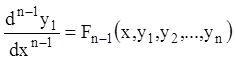 (1.56)
(1.56)
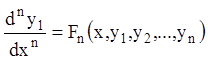 .
(1.57)
.
(1.57)
У такий спосіб одержимо ![]() тотожність:
тотожність:
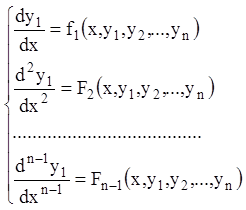 (1.58)
(1.58)
і ще одна тотожність (1.57).
Припустимо, що в розглянутій області зміни змінних, визначник
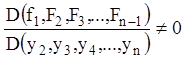 .
(1.59)
.
(1.59)
Тоді систему (1.58) можна розв'язати відносно ![]() ,
виразивши їх через змінні
,
виразивши їх через змінні ![]() . Підставивши знайдені
із системи (1.58) змінні
. Підставивши знайдені
із системи (1.58) змінні ![]() в рівняння (1.57), одержимо
рівняння
в рівняння (1.57), одержимо
рівняння ![]() -го порядку:
-го порядку:
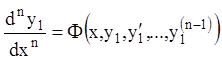 ,
(1.60)
,
(1.60)
якому задовольняє функція ![]() , що є по припущенню функцією
, що є по припущенню функцією ![]() розв’язання
розв’язання ![]() системи
(1.52).
системи
(1.52).
Доведемо тепер, що якщо взяти будь-яке розв'язання ![]() побудованого рівняння (1.60), підставити
його в систему (1.60) і визначити із цієї системи
побудованого рівняння (1.60), підставити
його в систему (1.60) і визначити із цієї системи ![]() , то система
функцій
, то система
функцій
![]() (1.61)
(1.61)
буде розв'язанням системи (1.52).
Підставивши знайдену систему функцій (1.61) у систему (1.58), оберне рівняння в тотожності, зокрема:
 .
(1.62)
.
(1.62)
Диференціюючи останню тотожність по ![]() ,
одержимо:
,
одержимо:
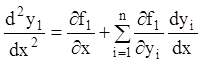 .
(1.63)
.
(1.63)
У цій тотожності поки не можна замінити ![]() на
на ![]() , тому що треба довести, що отримані з
рівняння (1.60) і системи (1.58) функції
, тому що треба довести, що отримані з
рівняння (1.60) і системи (1.58) функції ![]() задовольняють
системі (1.52).
задовольняють
системі (1.52).
Віднімаючи з тотожності (1.63) другу тотожність системи (1.58), що має вид (1.53), одержуємо:
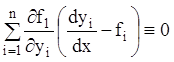 ,
,
або в силу першого рівняння
системи (1.58) 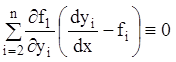 . Аналогічно, диференціюючи другу
тотожність системи (1.58) і віднімаючи з нього (1.55), написане в розгорнутому
виді, одержуємо:
. Аналогічно, диференціюючи другу
тотожність системи (1.58) і віднімаючи з нього (1.55), написане в розгорнутому
виді, одержуємо:
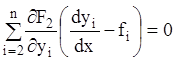 ;
;
. . . . . . . . . . . . . . . . . . . . . .
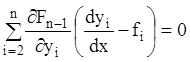 .
.
Розглянемо лінійну однорідну систему
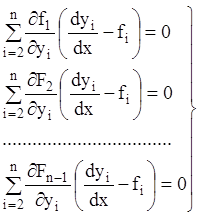 (1.64)
(1.64)
с ![]() -м
невідомим
-м
невідомим 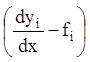
![]() . Її
визначник збігається з відмінним від нуля функціональним визначником (1.59):
. Її
визначник збігається з відмінним від нуля функціональним визначником (1.59):
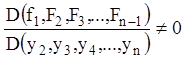 ,
,
і тоді однорідна система (1.64) у кожній точці розглянутої області має єдине тривіальне розв'язання.
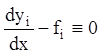
![]() .
.
Тоді, беручи до уваги (1.62), одержуємо, що ![]() функцій
функцій
![]() є розв'язанням системи рівнянь (1.52).
є розв'язанням системи рівнянь (1.52).
Зауваження 1.Процес
виключення функцій ![]() (крім
(крім ![]() )
припускає, що функціональний визначник
)
припускає, що функціональний визначник 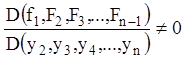 . Якщо
ця умова не виконана, то виключають якусь іншу з функцій
. Якщо
ця умова не виконана, то виключають якусь іншу з функцій ![]() , для якої відповідний функціональний
визначник не дорівнює нулю.
, для якої відповідний функціональний
визначник не дорівнює нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.