Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 2

Усяка інтегральна крива системи (1.4) володіє тою чудовою властивістю, що в кожній її точці напрямок дотичною збігається з напрямком поля, визначеного системою (1.4) у цій точці.

Справді, записавши нормальну систему (1.4) у вигляді:

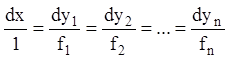                                                     (1.9)

і підставивши замість  розв'язання (1.2) системи (1.4), ми будемо мати рівняння дотичної до інтегральної кривої (1.2), причому відрізки поля напрямків є відрізками цієї дотичної в кожній точці поля.

Якщо в точці  всі праві частини системи (1.4) або деякі з них звертаються в невизначеність , то говорять, що в цій точці поле не визначене. Будемо вважати, що через таку точку не проходить жодна інтегральна крива системи (1.4). Якщо інтегральна крива (1.2) володіє тою властивістю, що , , ...,  при , то говорять, що ця інтегральна крива примикає до точки .

Можна дати й механічне тлумачення нормальної системи (1.4) і її розв'язку (1.2). Будемо розглядати незалежну змінну  як час, а систему значень невідомих функцій , , ...,  як координати точки  - мірного простору, яке називається фазовим простором . Тоді система (1.4) має вигляд:

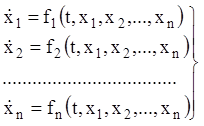.                                                       (1.10)

Ця система визначає в кожен момент часу  в даній точці фазового простору  компоненти швидкості  точки, що рухається.

Задача знаходження розв'язання системи (1.10) складається у визначенні величин , , ..., , якщо дано, що при  координати мали початкові значення . Або іншими словами знайти функції

, ..., .                                     (1.11)

Звичайно при такому тлумаченні система (1.10) називається динамічною, а кожне її розв'язання (1.11) –рухом. Крива, описувана точкою при русі, називається траєкторією руху. Рівняння (1.11) – параметричні рівняння траєкторії руху. Вони визначають траєкторію як геометричне місце точок, але, визначаючи положення точки на траєкторії в будь-який момент часу, показують, як відбувається рух точки по траєкторії із часом.

Найбільший інтерес становить випадок автономної системи (1.6). Рівняння цієї системи визначають стаціонарний рух середовища, швидкість у кожній точці простору не залежить від часу й, отже, є постійною в цій точці протягом усього часу. Розв'язання (1.11) залежить від  довільних постійних  – координат початкового положення точки, траєкторія якої розглядається.

Якщо всі функції   в рівняннях руху (1.11) являють собою константи , , ..., , той рух (1.11) вироджується в стан спокою

, , ..., ,

а його траєкторія – у точку .

Висновок: основною задачею інтегрування системи (1.10) є знаходження всіх рухів, обумовлених цією системою, і вивчення їхніх властивостей.

Приклад. Розв’язати систему .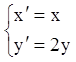

Розв'язання.

.

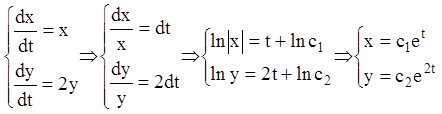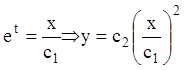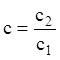
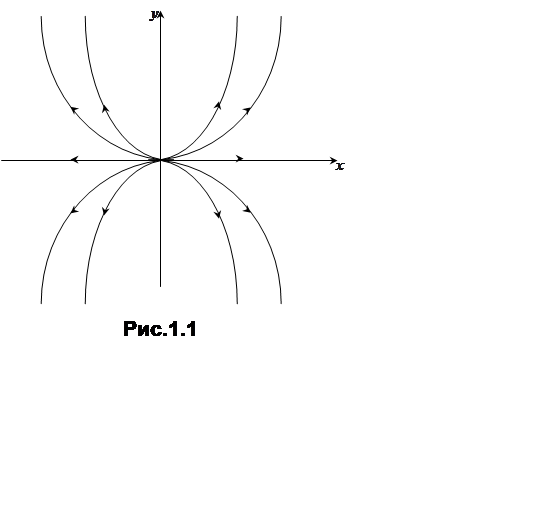
Таким чином, ця система визначає сімейство рухів виду , , де  й  – довільні постійні. Для одержання траєкторії виключаємо із сімейства рухів параметр :  або , де  . Тобто траєкторіями цих рухів служать напівпараболи  , півосі координат і початок координат (на малюнку стрілки вказують напрямок рухів при зростанні ).

1.3 Задача Коші й теорема існування для нормальної системи

Для нормальної системи (1.4)задача Кошіставиться так: серед всіх розв'язків (1.4) знайти таке:

, , ..., ,                                     (1.12)

у якому функції   при заданому значенні незалежної змінної  приймають задані значення, тобто:

, , ..., .                                (1.13)

При цьому  називають, відповідно, початковими значеннями незалежної змінної й шуканої функцій, а умови (1.13) – початковими умовами задачі Коші.

Геометричне тлумачення задачі Коші: серед всіх інтегральних кривих системи (1.4) знайти ту, котра проходить через задану точку .

Механічне тлумачення задачі Коші для нормальної системи (1.10) з початковими умовами

, , ..., :                                  (1.14)

із всіх рухів, обумовлених системою (1.10), знайти такий рух

, , ..., ,                                        (1.15)