Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 7

Зауваження 2. Якщо розв'язувана система є лінійною однорідною (або неоднорідною) системою, то отримане в результаті виключення рівняння (1.60) теж буде лінійним однорідним (або неоднорідним) рівнянням -го порядку. Причому якщо всі коефіцієнти лінійної системи були постійними, то отримане лінійне рівняння теж буде з постійними коефіцієнтами.

Приклад.Проінтегрувати методом виключення систему:

.

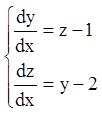Розв'язання. З першого рівняння виражаємо  через .

                                                                 (1.65)

Продиференціював (1.65) по , одержимо  й підставимо це значення  в друге рівняння вихідної системи. Одержуємо

                                                                 (1.66)

або . Це лінійне неоднорідне диференціальне рівняння другого порядку з постійними коефіцієнтами. Розв’язуємо його. Загальне розв'язання неоднорідного рівняння шукаємо у вигляді ,  – очевидне розв'язання. . Характеристичне рівняння ; ; . Тоді  й

.                                                        (1.67)

Функцію  знаходимо, підставляючи (1.67) в (1.65), попередньо обчисливши . Тоді .

Відповідь: , .

Приклад.Розв’язати систему:

.

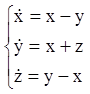Розв'язання. Послідовно диференціюємо перше рівняння й підставляємо замість  їхнього значення із системи.  , тобто, тобто . Віднімаючи із третього підкресленої рівності друге, одержуємо . Це лінійне однорідне рівняння третього порядку. Характеристичне рівняння:

 або , тобто , .

.

Тоді з першої підкресленої рівності одержуємо:

,

тобто . Із другої підкресленої рівності одержуємо:

.

Відповідь: , , .

Зауваження. Метод виключення використовується також при розв'язанні канонічних систем диференціальних рівнянь (1.51), які зводяться до одного рівняння -го порядку.

Приклад.Знайти розв'язання системи 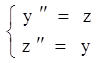, що задовольняє початковим умовам , , , .

Розв'язання. Продиференціюємо перше рівняння

і замість  підставимо її значення із другого рівняння. Одержимо . Характеристичне рівняння

  ; , , .

Тоді . Двічі продиференціював останню рівність і з огляду на перше рівняння, знаходимо .

   .

.

З огляду на початкові умови, одержуємо:

, , , .

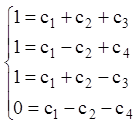
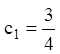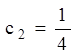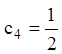Тоді шукане розв'язання запишеться:

.

1.6.3. Метод інтегрувальних комбінацій

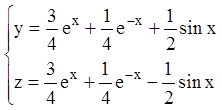Інтегрувальною комбінацією називають диференціальне рівняння, що є наслідком рівнянь системи

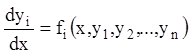
                                              (1.68)

але легко інтегрується. Наприклад, рівняння

або рівняння, що зводяться заміною змінних до інтегрувального типу диференціальних рівнянь із однією невідомою функцією. Безпосередній метод інтегрування зводиться до утворення за допомогою додавання, вирахування, ділення даних рівнянь легко інтегрувальних рівнянь (інтегрувальних комбінацій), отриманих з даної системи, виду

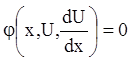,                                                   (1.69)

де  – деяка функція від шуканих функцій , не утримуюча . У випадку лінійної однорідної системи з постійними коефіцієнтами інтегрувальна комбінація є диференціальне рівняння з розділеними змінними, у випадку лінійної неоднорідної системи - лінійне диференціальне рівняння першого порядку. Кожна інтегрувальна комбінація дає один перший інтеграл, якщо їхнє число дорівнює числу рівнянь системи, то інтегрування закінчене, у противному випадку виходить система з меншим числом невідомих функцій.

Часто буває корисно нормальну систему (1.68) записати в симетричній формі

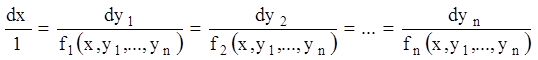.               (1.70)

Далі шукаємо такі комбінації членів рівностей (7.70), лінійні щодо диференціалів, щоб у лівій частині стояв повний диференціал, а в правої – нуль. Інтегруючи цей повний диференціал і дорівнюючи результат постійної , одержуємо перший інтеграл. Якщо таким шляхом знайдено  незалежних інтегралів, задача знаходження загального розв'язання зводиться до інтегрування диференціального рівняння першого порядку.

Зауваження.При знаходженні перших інтегралів системи (1.70) можна використовувати властивість ряду рівних відносин (або похідні пропорції):

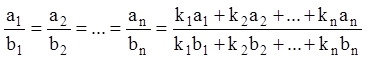                               (1.71)