Теорема 6. Якщо ![]() розв'язань
розв'язань ![]() ЛОС
лінійно незалежні в інтервалі неперервності коефіцієнтів системи
ЛОС
лінійно незалежні в інтервалі неперервності коефіцієнтів системи ![]() , то їхній визначник Вронського не
звертається в нуль у жодній точці цього інтервалу.
, то їхній визначник Вронського не
звертається в нуль у жодній точці цього інтервалу.
Доказ аналогічно подібній до теореми для лінійних однорідних рівнянь.
Таким чином, для лінійної незалежності ![]() розв'язань
лінійної однорідної системи в інтервалі неперервності її коефіцієнтів
розв'язань
лінійної однорідної системи в інтервалі неперервності її коефіцієнтів ![]() необхідно й досить, щоб їх
необхідно й досить, щоб їх ![]() був відмінний від нуля хоча б в одній
точці цього інтервалу.
був відмінний від нуля хоча б в одній
точці цього інтервалу.
Зазначені вище властивості (теореми 4,6) вронськіана розв'язань лінійної однорідної системи легко випливають із наступної формули Остроградського-Ліувиля, що виражає (з точністю до постійного множника) вронськіан розв'язань через діагональні коефіцієнти системи
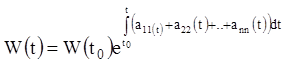 ,
(1.85)
,
(1.85)
де ![]() –
будь-яка точка з інтервалу неперервності
–
будь-яка точка з інтервалу неперервності ![]() коефіцієнтів
системи.
коефіцієнтів
системи.
Для доказу цієї формули обчислюють похідну від вронськіана,
диференціюючи по стовпцях. Тому що в цьому випадку похідна від визначника ![]() -го порядку дорівнює сумі
-го порядку дорівнює сумі ![]() визначників, що виходять із нього почерговою
заміною елементів 1-го, 2-го, ...,
визначників, що виходять із нього почерговою
заміною елементів 1-го, 2-го, ..., ![]() -го стовпця їхніми
похідними, то
-го стовпця їхніми
похідними, то
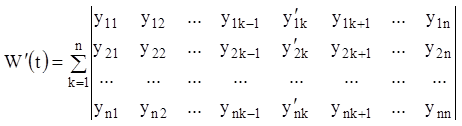 .
.
Заміняючи похідні ![]() їхніми значеннями з
тотожностей
їхніми значеннями з
тотожностей
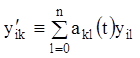
![]()
одержуємо праворуч:
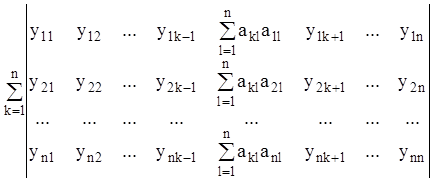 .
.
Розклавши визначник, що стоїть під знаком суми, на суму ![]() визначників відзначимо, що всі визначники,
що виходять, будуть дорівнюють нулю, крім визначника, що
визначників відзначимо, що всі визначники,
що виходять, будуть дорівнюють нулю, крім визначника, що ![]() відповідає (тому що кожний з них буде мати
два пропорційних стовпці). Визначник же, що відповідає
відповідає (тому що кожний з них буде мати
два пропорційних стовпці). Визначник же, що відповідає ![]() ,
дорівнює
,
дорівнює ![]() . Тому
. Тому
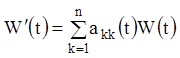 ,
,
звідки й треба формула Остроградського-Ліувиля (1.85).
Теорема 7. Лінійна комбінація 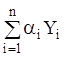 фундаментальної системи
розв'язань
фундаментальної системи
розв'язань ![]() однорідної системи
однорідної системи
![]() (1.86)
(1.86)
с
неперервними на ![]() коефіцієнтами
коефіцієнтами ![]() є загальним розв'язанням системи (1.86) на
тім же відрізку.
є загальним розв'язанням системи (1.86) на
тім же відрізку.
Доведення.Тому
що коефіцієнти ![]() неперервні при
неперервні при ![]() , те для системи (1.85) виконуються умови
теореми існування й одиничності, а в силу теорем 1 – 2 функція
, те для системи (1.85) виконуються умови
теореми існування й одиничності, а в силу теорем 1 – 2 функція 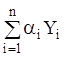 теж є розв'язанням системи (1.86), отже,
для доказу теореми досить обґрунтувати, що підбором постійних
теж є розв'язанням системи (1.86), отже,
для доказу теореми досить обґрунтувати, що підбором постійних ![]() у розв'язанні
у розв'язанні 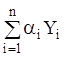 можна
задовольнити довільно обраним початковим умовам
можна
задовольнити довільно обраним початковим умовам ![]() , де
, де ![]() , де
, де ![]() –
довільне з відрізка
–
довільне з відрізка ![]() , тобто досить показати, що
векторне рівняння
, тобто досить показати, що
векторне рівняння
![]() (1.87)
(1.87)
завжди буде мати розв'язання
або буде мати розв'язання еквівалентна (1.87) система ![]() скалярних
рівнянь:
скалярних
рівнянь:
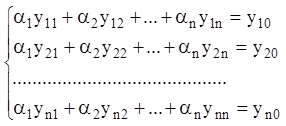 .
(1.88)
.
(1.88)
Система (1.88) розв'язна відносно ![]() при
будь-яких
при
будь-яких ![]() , тому що її визначник не дорівнює нулю при
, тому що її визначник не дорівнює нулю при
![]() як визначник Вронського фундаментальної
системи розв'язань
як визначник Вронського фундаментальної
системи розв'язань ![]() й, отже, загальне рішення має
вигляд
й, отже, загальне рішення має
вигляд 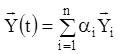 , де
, де ![]() –
фундаментальна система розв'язань.
–
фундаментальна система розв'язань.
Висновки. Якщо
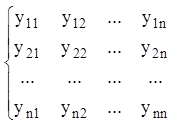 ,
,
побудована фундаментальна
системи розв'язань однорідної лінійної системи (1.86) на інтервалі
неперервності коефіцієнтів системи ![]() , то загальне
розв'язання системи записуємо у вигляді
, то загальне
розв'язання системи записуємо у вигляді
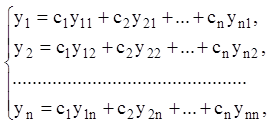
де ![]() –
довільні постійні, або в скороченому виді
–
довільні постійні, або в скороченому виді 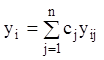
![]() .
.
Приклад.Побудувати загальне розв'язання системи
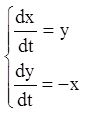 ,
,
якщо цій системі
задовольняють розв'язання ![]() ,
, ![]() ; і
; і ![]() ,
, ![]() .
.
Розв'язання. Ці розв'язання утворять фундаментальну систему, тому що визначник Вронського:
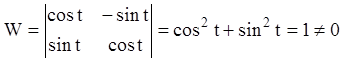 .
.
Отже загальне розв'язання має вигляд:
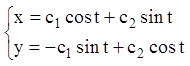 ,
,
де ![]() й
й
![]() – довільні постійні.
– довільні постійні.
Теорема 8.Якщо ![]() є розв'язанням
неоднорідної системи
є розв'язанням
неоднорідної системи
![]() ,
(1.89)
,
(1.89)
а ![]() –
розв'язанням відповідної однорідної системи
–
розв'язанням відповідної однорідної системи
![]() ,
(1.90)
,
(1.90)
то сума ![]() теж буде розв'язанням неоднорідної системи
(1.89).
теж буде розв'язанням неоднорідної системи
(1.89).
Доведення. З умови
треба, що ![]() й
й ![]() . Тоді,
використовуючи властивість 2 лінійні оператори
. Тоді,
використовуючи властивість 2 лінійні оператори ![]() ,
одержуємо
,
одержуємо ![]() , тобто
, тобто![]() , що й
було потрібно довести.
, що й
було потрібно довести.
Теорема 9. Загальне
розв'язання на ![]() неоднорідної системи з
неперервними на
неоднорідної системи з
неперервними на ![]() коефіцієнтами
коефіцієнтами ![]() й правими частинами
й правими частинами ![]() дорівнює сумі загального розв'язання
дорівнює сумі загального розв'язання 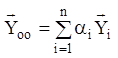 відповідної однорідної системи й
частинного розв'язання
відповідної однорідної системи й
частинного розв'язання ![]() неоднорідної системи, тобто
неоднорідної системи, тобто![]() .
.
Доведення.Тому
що умови теореми існування й одиничності виконані, і з теореми 6 треба, що ![]() буде розв'язанням неоднорідної системи, то
для доказу теореми досить довести, що в розв'язанні
буде розв'язанням неоднорідної системи, то
для доказу теореми досить довести, що в розв'язанні
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.